Soạn giáo án điện tử toán 10 chân trời bài 4: Tích vô hướng của hai vecto

Nội dung giáo án

CHÀO MỪNG CÁC EM ĐẾN TIẾT HỌC HÔM NAY!

KHỞI ĐỘNG

Tác dụng của một lực  vào một vật làm cho vật đó dịch chuyển theo vectơ  thì sẽ sinh ra một công là A. Công A đó được tính theo công thức như thế nào?  là góc giữa hai vectơ  và .

cos

CHƯƠNG V: VECTƠ

BÀI 4: TÍCH VÔ HƯỚNG CỦA HAI VECTO

NỘI DUNG BÀI HỌC

Góc giữa hai vectơ

Tích vô hướng của hai vectơ

Tính chất của tích vô hướng

Góc giữa hai vectơ

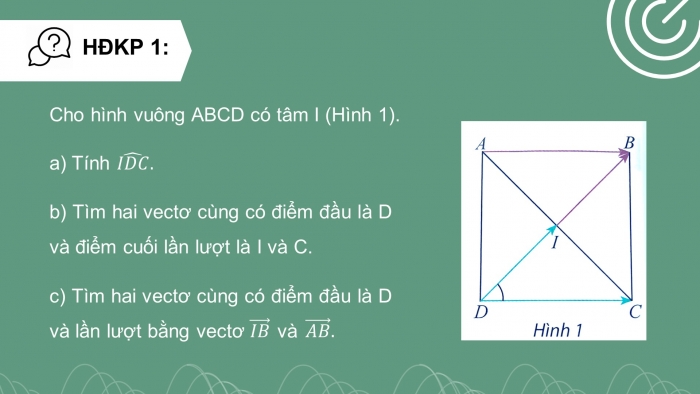
HĐKP 1:

Cho hình vuông ABCD có tâm I (Hình 1).

1. a) Tính 
2. b) Tìm hai vectơ cùng có điểm đầu là D và điểm cuối lần lượt là I và C.
3. c) Tìm hai vectơ cùng có điểm đầu là D và lần lượt bằng vectơ và

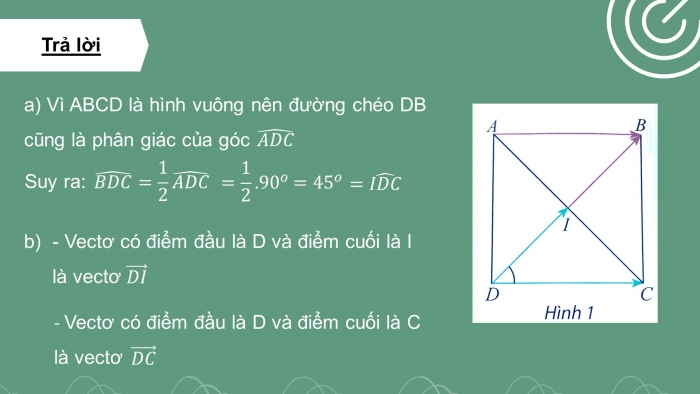
Trả lời

1. a) Vì ABCD là hình vuông nên đường chéo DB cũng là phân giác của góc

Suy ra:

• - Vectơ có điểm đầu là D và điểm cuối là I là vectơ
• - Vectơ có điểm đầu là D và điểm cuối là C là vectơ

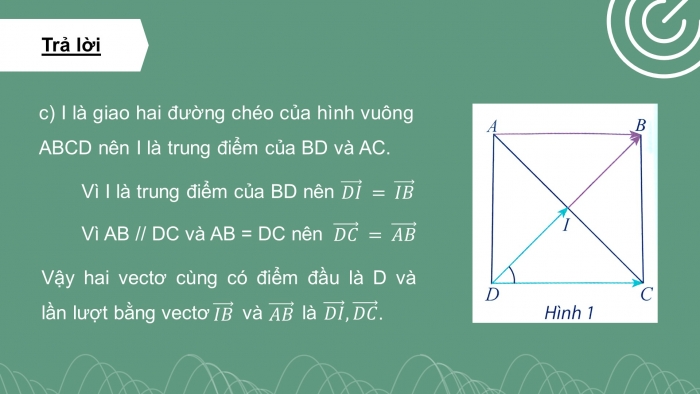
Trả lời

1. c) I là giao hai đường chéo của hình vuông ABCD nên I là trung điểm của BD và AC.

Vì I là trung điểm của BD nên

Vì AB // DC và AB = DC nên

Vậy hai vectơ cùng có điểm đầu là D và   lần lượt bằng vectơ      và         là

KẾT LUẬN

Cho hai vectơ  khác  khác . Từ một điểm O bất kì ta vẽ  = ;  =

Góc  với số  đo từ  đến  được gọi là góc giữa hai vectơ  và .

Ta kí hiệu góc giữa hai vectơ  và  là ( , ).

Nếu ( , ) =  thì ta nói rằng và  vuông góc với nhau, kí hiệu  

* Chú ý:

• Từ định nghĩa ta có: = .
• Góc giữa hai vectơ cùng hướng và khác luôn bằng .
• Góc giữa hai vectơ ngược hướng và khác luôn bằng .
• Trong trường hợp có ít nhất một trong hai vectơ và  là vectơ  thì ta quy ước số đo góc giữa hai vectơ đó tùy ý (từ  đến ).

Ví dụ 1 (SGK – tr98)

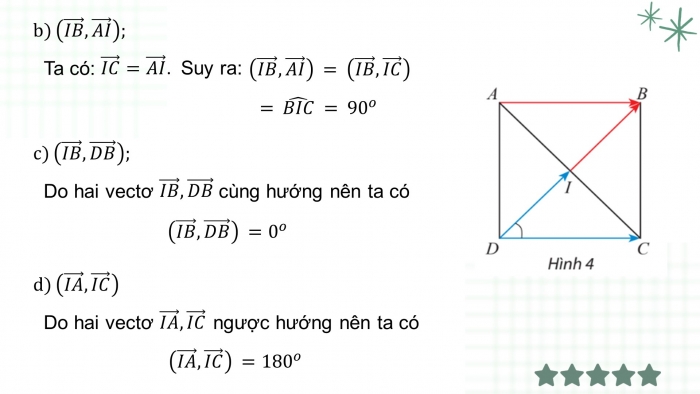
Cho hình vuông ABCD có tâm I là giao điểm của hai đường chéo. Tìm các góc:

Giải

Ta có:

Suy ra: