Soạn giáo án điện tử toán 10 chân trời bài 1: Khái niệm vectơ

Nội dung giáo án

CHÀO MỪNG CÁC EM ĐẾN VỚI TIẾT HỌC HÔM NAY

KHỞI ĐỘNG

Chiếc máy bay đang bay theo một hướng nhất định, với vận tốc v. Với một đơn vị đo chẳng hạn như km/h thì ta có thể biểu diễn được độ lớn của vận tốc. Nhưng có đại lượng nào có thể biểu diễn được cả hướng và độ lớn hay không?

CHƯƠNG V: VECTƠ

BÀI 1: KHÁI NIỆM VECTƠ

NỘI DUNG

Định nghĩa vectơ

Hai vectơ cùng phương, cùng hướng

Vectơ bằng nhau - Vectơ đối nhau. Vectơ-không

Luyện tập

Định nghĩa vectơ

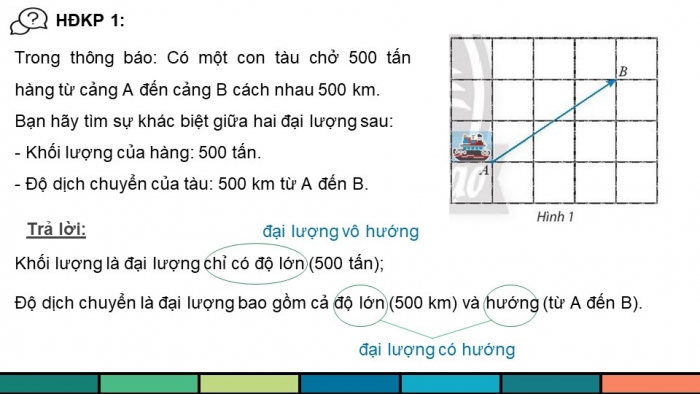
HĐKP 1:

Trong thông báo: Có một con tàu chở 500 tấn hàng từ cảng A đến cảng B cách nhau 500 km.

Bạn hãy tìm sự khác biệt giữa hai đại lượng sau:

- Khối lượng của hàng: 500 tấn.

- Độ dịch chuyển của tàu: 500 km từ A đến B.

Trả lời:

Khối lượng là đại lượng chỉ có độ lớn (500 tấn);

Độ dịch chuyển là đại lượng bao gồm cả độ lớn (500 km) và hướng (từ A đến B).

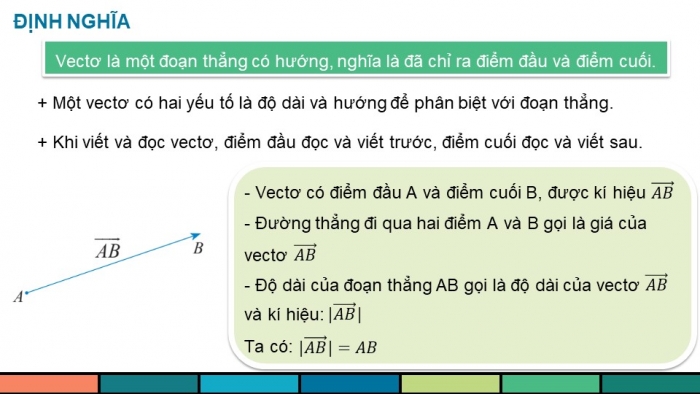
ĐỊNH NGHĨA

Vectơ là một đoạn thẳng có hướng, nghĩa là đã chỉ ra điểm đầu và điểm cuối.

+ Một vectơ có hai yếu tố là độ dài và hướng để phân biệt với đoạn thẳng.

+ Khi viết và đọc vectơ, điểm đầu đọc và viết trước, điểm cuối đọc và viết sau.

- Vectơ có điểm đầu A và điểm cuối B, được kí hiệu

- Đường thẳng đi qua hai điểm A và B gọi là giá của

vectơ

- Độ dài của đoạn thẳng AB gọi là độ dài của vectơ

và kí hiệu:

Viết các vecto sau dưới dạng kí hiệu

* Chú ý: Một vectơ khi không cần chỉ rõ điểm đầu và điểm cuối có thể viết là ; , , ,...

* Hai điểm A, B phân biệt thì tạo ra hai vectơ là : .

Ví dụ 1 (SGK – tr82)

Cho tam giác đều ABC có cạnh bằng 2. Gọi H là trung điểm của đoạn thẳng BC.

Tìm điểm đầu, điểm cuối, giá và độ dài của các vecto:

+ Vecto  có điểm đầu là C, điểm cuối là A và có giá là đường thẳng AC.

+ Vecto  có điểm đầu là A, điểm cuối là H và có giá là đường thẳng AH.

+ Vecto  có điểm đầu là B, điểm cuối là H và có giá là đường thẳng BH.

Ta có:

THỰC HÀNH 1

Tìm điểm đầu, điểm cuối, giá và độ dài của các vectơ  trong Ví dụ 1.

+ Vectơ  có điểm đầu là C, điểm cuối là H và có giá là đường thẳng CH.

+ Vectơ  có điểm đầu là C, điểm cuối là B và có giá là đường thẳng CB.

+ Vectơ  có điểm đầu là H, điểm cuối là A và có giá là đường thẳng HA.

Ta có: CH = 1; AH =  =  =

 | | = 1; | | = 2; | | =

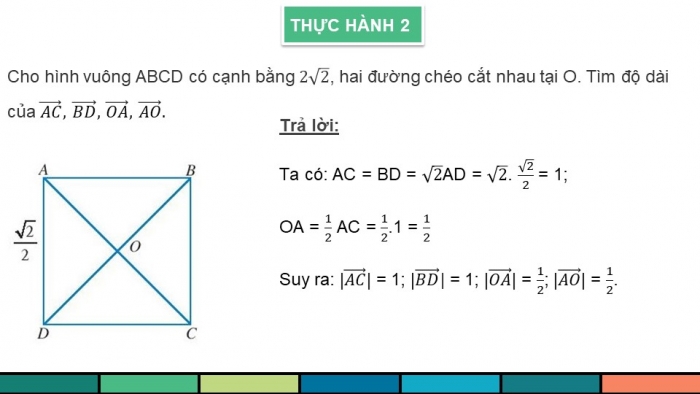
THỰC HÀNH 2

Cho hình vuông ABCD có cạnh bằng  , hai đường chéo cắt nhau tại O. Tìm độ dài của 

Ta có: AC = BD = AD = .  = 1;

OA =  AC = .1 =

Suy ra: | | = 1; |  = 1; | | = ; | | = .

Hai vectơ cùng phương, cùng hướng

Bạn có nhận xét gì về giá của các cặp vectơ   và  ,  và   trong Hình?

Giá của vectơ  là đường thẳng AB, giá của vectơ  là đường thẳng CD.

 Giá của vectơ  trùng với giá của vectơ .

Tương tự, giá của vectơ  song song với giá của vectơ .

KẾT LUẬN

Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

Nhận xét: Hai vectơ cùng phương chỉ có thể cùng hướng hoặc ngược hướng.

Ví dụ 3 (SGK – tr83)

Tìm các cặp lực ngược hướng trong số các lực tác động vào máy bay trong Hình.

Trả lời:

Lực  ngược hướng với trọng lực ;

Lực cản  ngược hướng với lực đẩy .

THỰC HÀNH 3

Quan sát Hình 8 và gọi tên các vectơ:

1. a) Cùng phương với vectơ  ;
2. b) Cùng hướng với vectơ  ;
3. c) Ngược hướng với vectơ  .

Trả lời:

1. a) Cùng phương với vectơ là: ; ; .
2. b) Cùng hướng với vectơ là: .
3. c) Ngược hướng với vectơ là: .

Nhận xét: Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi hai vectơ  và  cùng phương.

THỰC HÀNH 4

Khẳng định sau đây đúng hay sai? Hãy giải thích.

Nếu ba điểm phân biệt A, B, C thẳng hàng thì hai vectơ              cùng hướng.

Khẳng định sau đây đúng hay sai? Hãy giải thích.

Nếu ba điểm phân biệt A, B, C thẳng hàng thì hai vectơ              cùng hướng.

Khẳng định sai.

Vì đề bài không nêu rõ ba điểm phân biệt A, B, C thẳng hàng theo thứ tự nào, nên nếu A nằm giữa B và C thì hai vectơ   và   ngược hướng.

Vectơ bằng nhau - Vectơ đối nhau.

Vectơ-không

3. Vectơ bằng nhau - Vectơ đối nhau

HĐKP 3:

Cho hình bình hành ABCD (hình 10), hãy so sánh độ dài và hướng của hai vectơ:

 và

 và

Trả lời:

1. a) Hai vec tơ và cùng hướng và có độ dài bằng nhau.
2. b) Hai vec tơ và ngược hướng và có độ dài bằng nhau.

KẾT LUẬN

+ Hai vectơ  và  được gọi là bằng nhau nếu chúng có cùng hướng và có cùng độ dài, kí hiệu là  = .

+ Hai vectơ  và  được gọi là đối nhau nếu chúng ngược hướng và có cùng độ dài, kí hiệu  = - . Khi đó, vectơ  được gọi là vectơ đối của vectơ .

Cho trước một vectơ  và điểm O, có bao nhiêu điểm A sao cho ? Vì sao?

Nếu có đoạn thẳng MN thì nhận xét mối quan hệ của hai vectơ ?

Chú ý:

1. a) Cho vectơ và điểm O, ta luôn tìm được một điểm A duy nhất sao cho = .

Khi đó, độ dài của vectơ  là độ dài đoạn OA, kí hiệu là | |.

1. b) Cho đoạn thẳng MN, ta luôn có = - .

Ví dụ 4 (SGK – tr85)

1. Tìm trong Hình 10 hai cặp vectơ bằng nhau và hai cặp vectơ đối nhau.
2. Cho điểm O là trung điểm của đoạn thẳng AB. Tìm hai vectơ đối nhau.

Trả lời:

1. a) Trong Hình 10, ta có:

(Hình 13)

THỰC HÀNH 5

Cho D, E, F lần lượt là trung điểm của các cạnh BC, CA và AB của tam giác ABC (Hình 14).

1. Tìm các vectơ bằng vectơ  .
2. Tìm các vectơ đối của vectơ  .

Trả lời:

1. a) Các vectơ bằng vectơ là: ;
2. b) Các vectơ đối của vectơ là ; .
3. Vectơ-không

Khái niệm:

Vectơ có điểm đầu và điểm cuối trùng nhau gọi là vectơ-không, kí hiệu là .

Chú ý:

+ Quy ước vectơ-không có độ dài bằng 0.

+ Vectơ-không luôn cùng phương, cùng hướng với mọi vectơ.

+ Mọi vectơ-không đều bằng nhau  =  =  =  = ...     với mọi điểm A, B, C,...

+ Vectơ đối của vectơ-không là chính nó.