Soạn giáo án điện tử toán 10 chân trời bài 2: Hoán vị, chỉnh hợp và tổ hợp

Nội dung giáo án

CHÀO MỪNG TẤT CẢ CÁC EM ĐÃ ĐẾN VỚI TIẾT HỌC HÔM NAY!

KHỞI ĐỘNG

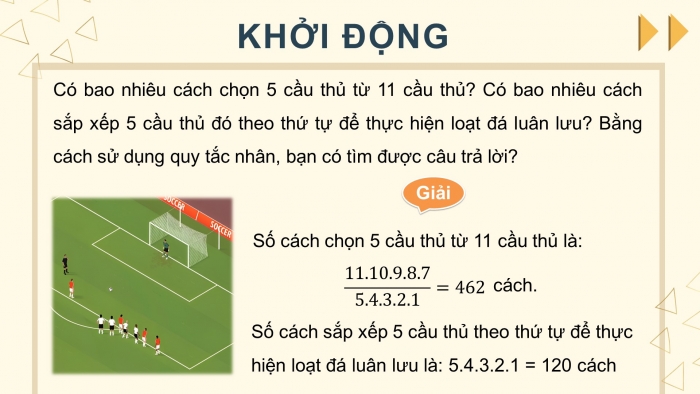
Có bao nhiêu cách chọn 5 cầu thủ từ 11 cầu thủ? Có bao nhiêu cách sắp xếp 5 cầu thủ đó theo thứ tự để thực hiện loạt đá luân lưu? Bằng cách sử dụng quy tắc nhân, bạn có tìm được câu trả lời?

Giải

Số cách chọn 5 cầu thủ từ 11 cầu thủ là:

Số cách sắp xếp 5 cầu thủ theo thứ tự để thực hiện loạt đá luân lưu là: 5.4.3.2.1 = 120 cách

CHƯƠNG VIII.ĐẠI SỐ TỔ HỢP

BÀI 2: HOÁN VỊ, CHỈNH HỢP VÀ TỔ HỢP

NỘI DUNG BÀI HỌC

Hoán vị

Chỉnh hợp

Tổ hợp

Tính số các hoán vị, chỉnh hợp, tổ hợp bằng máy tính cầm tay

Hoán vị

  Thảo luận nhóm, hoàn thành HĐKP1.

Sau giờ thực hành trải nghiệm, ba đội A, B, C bốc thăm để xác định thứ tự trình bày, thuyết minh về sản phẩm của mỗi đội.

1. a) Hãy liệt kê tất cả các kết quả bốc thăm có thể xảy ra.
2. b) Có tất cả bao nhiêu kết quả như vậy? Ngoài các đếm lần lượt từng kết quả, có cách nào tìm nhanh hơn không?

Giải

1. a) Tất cả các kết quả bốc thăm có thể xảy ra là:

ABC;  ACB; BAC ; BCA; CAB ; CBA.

1. b) Từ câu a) ⇒ có tất cả 6 kết quả như vậy.

Ngoài cách đếm lần lượt từng kết quả, ta có cách sau:

• CĐ1: Chọn 1 trong 3 đội xếp vào vị trí thứ nhất, có 3 cách chọn.
• CĐ2: Chọn 1 trong 2 đội còn lại xếp vào vị trí thứ hai, có 2 cách chọn.
• CĐ3: Xếp đội còn lại vào vị trí thứ ba.

Áp dụng quy tắc nhân có: 3.2.1 = 6 kết quả khác nhau có thể xảy ra.

KẾT LUẬN

• Cho tập hợp A có n phần tử ( 1). Mỗi cách sắp xếp n phần tử của A theo một thứ tự gọi là một "hoán vị" các phần tử đó (gọi tắt là hoán vị của A hay n phần tử).
• Kí hiệu: P_n - số hoán vị của n phần tử.
• Số hoán vị của n phần tử ( 1) bằng:

CHÚ Ý

• Ta đưa vào kí hiệu:

     và đọc là n giai thừa hoặc giai thừa của n.

     Khi đó, P_n = n!

• Quy ước: 0! = 1

Ví dụ 1 (SGK – tr27)

Bãi đỗ xe ô tô còn lại ba chỗ trống như Hình 1. Có ba chiếc ô tô (kí hiệu  ) đang đi vào bãi để đỗ xe.

1. a) Có bao nhiêu cách sắp xếp ba chiếc xe vào ba chỗ trống?
2. b) Vẽ sơ đồ hình cây về các cách sắp xếp và kiểm tra kết quả tính toán ở trên.

Giải

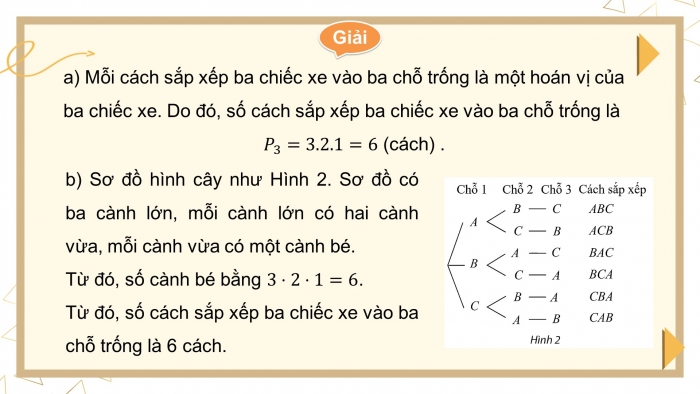
1. a) Mỗi cách sắp xếp ba chiếc xe vào ba chỗ trống là một hoán vị của ba chiếc xe. Do đó, số cách sắp xếp ba chiếc xe vào ba chỗ trống là
2. b) Sơ đồ hình cây như Hình 2. Sơ đồ có ba cành lớn, mỗi cành lớn có hai cành vừa, mỗi cành vừa có một cành bé.

Từ đó, số cành bé bằng .

Từ đó, số cách sắp xếp ba chiếc xe vào ba chỗ trống là 6 cách.