Trong mỗi hình sau (H.4.33) có các cặp tam giác vuông nào bằng nhau? Vì sao?

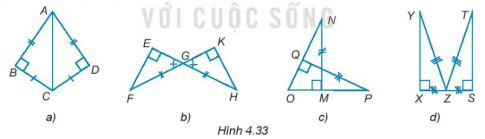
+) Hình a:

Xét $\Delta ABC$ và $\Delta ADC$ ta có:  

AB  = AD (giả thiết)

$\widehat{ABC}=\widehat{ADC}=90^{\circ}$ (giả thiết)

BC = CD (giả thiết)

Do đó, $\Delta ABC = \Delta ADC$ (hai cạnh góc vuông).

+) Hình b

Xét $\Delta EFG$ và $\Delta KHG$ ta có:

GF = GH (giả thiết)

$\widehat{FEG}=\widehat{HKG}=90^{\circ}$ (giả thiết)

$\widehat{EGF}=\widehat{HGK}$ (hai góc đối đỉnh)

Do đó, 4\Delta EFG =\Delta  KHG$ (góc nhọn – cạnh huyền)

+) Hình c:

Tam giác OMN vuông tại M nên $\widehat{ONM}+\widehat{O}=90^{\circ} =>\widehat{ONM}=90^{\circ}-\widehat{O}$

Tam giác OQP vuông tại Q nên $\widehat{OPQ}+\widehat{O}=90^{\circ}=>\widehat{OPQ}=90^{\circ}-\widehat{O}$

Do đó, $\widehat{ONM}=\widehat{OPQ}$.

Xét $\Delta OMN$ và $\Delta OQP$ ta có:

MN = PQ (giả thiết)

$\widehat{OMN}=\widehat{OQP}=90^{\circ}$ (giả thiết)

$\widehat{ONM}=\widehat{OPQ}$ (chứng minh trên)

Do đó, $\Delta OMN = \Delta OQP$ (góc nhọn – cạnh góc vuông).

+) Hình d:

Xét $\Delta XYZ$ và $\Delta STZ$ ta có:

YZ = TZ (giả thiết)

$\widehat{YXZ}=\widehat{TSZ}=90^{\circ}$ (giả thiết)

XZ = SZ (giả thiết)

Do đó, $\Delta XYZ = \Delta STZ$ (cạnh huyền – cạnh góc vuông).