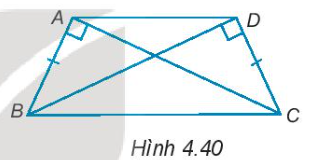
Cho bốn điểm A, B, C, D như Hình 4.40, trong đó AB = DC.

a) Gọi giao điểm của AC và BD là O.

Xét $\Delta ABC$ và $\Delta DCB$ có:

$\widehat{BAC}=\widehat{CDB}=90^{\circ}$ (giả thiết)

AB = CD (giả thiết)

BC chung

Do đó, $\Delta ABC = \Delta DCB$ (cạnh huyền – cạnh góc vuông).

Suy ra, AC = BD (hai cạnh tương ứng).

b) Vì $\Delta ABC = \Delta DCB$ nên $\widehat{ACB}=\widehat{DBC}$ (hai góc tương ứng)

Xét tam giác OBC có:  

$\widehat{OCB}+\widehat{CBO}+\widehat{BOC}=180^{\circ}$.

Mà $\widehat{OCB}=\widehat{CBO}$ do $\widehat{ACB}=\widehat{DBC}$ nên $2\widehat{CBO}+\widehat{BOC}=180^{\circ}$.

Suy ra $2\widehat{CBO}=180^{\circ}-\widehat{BOC}$

Do đó, $\widehat{CBO}=\frac{180^{\circ}-\widehat{BOC}}{2}$ (1)

Xét $\Delta ABD$ và $\Delta DCA$ có:  

AB = CD (giả thiết)

BD = AC (chứng minh trên)

AD chung

Do đó, $\Delta ABD = \Delta DCA$ (c.c.c).

Suy ra, $\widehat{ADB}=\widehat{DAC}$

Xét tam giác OAD có:

$\widehat{OAD}+\widehat{ADO}+\widehat{AOD}=180^{\circ}$.

Mà $\widehat{OAD}=\widehat{ADO}$ do $\widehat{ADB}=\widehat{DAC}$ nên $2\widehat{ADO}+\widehat{AOD}=180^{\circ}$

Suy ra $2\widehat{ADO}=180^{\circ}-\widehat{AOD}$

Do đó, $\widehat{ADO}=\frac{180^{\circ}-\widehat{AOD}}{2}$ (2)

Mà $\widehat{AOD}=\widehat{BOC}$ (hai góc đối đỉnh) (3)

Từ (1), (2), (3) suy ra, $\widehat{CBO}=\widehat{ADO}$ hay $\widehat{CBD}=\widehat{ADB}$.

Mà hai góc này ở vị trí so le trong nên AD // BC.