Giải bài tập 9.23 trang 59 SBT toán 7 tập 2 kết nối

a)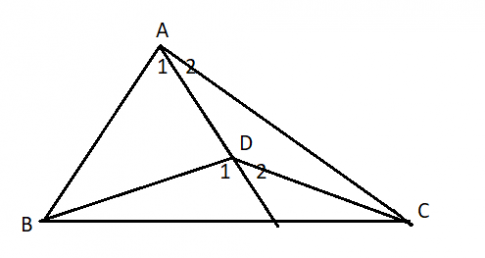 

Tia AD chia góc A thành góc A₁ và góc A₂, chia góc BDC thành góc D₁ và góc D₂.

Góc D₁ là góc ngoài tại đỉnh D của tam giác ABD nên:

$\widehat{D1}>\widehat{A1}$

Góc D₂ là góc ngoài tại đỉnh D của tam giác ADC nên:

$\widehat{D2}>\widehat{A1}$

=> $\widehat{D}=\widehat{D1}+\widehat{D2}>\widehat{A1}+\widehat{A2}=\widehat{A}$

b)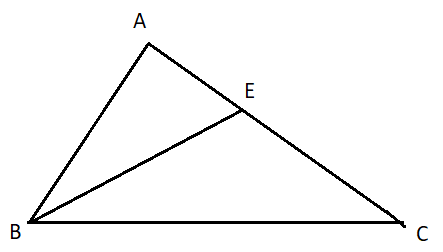 

Gọi E là giao điểm của BD và AC. Ta có:

AB + AC = AB + (AE + EC) = (AB + AE) + EC

Mà: AB + AE > BE (bất đẳng thức trong tam giác ABE)

=>(AB + AE) + EC > BE + EC = (BD + DE) + EC = BD + (DE + EC)

Mà DE + EC > DC (bất đẳng thức trong tam giác DEC)

=>AB + AC > BD + DC.