Giải bài tập 6 trang 73 sgk Toán 8 tập 2 CD
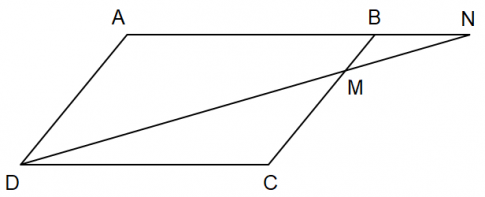
Bài tập 6 trang 73 sgk Toán 8 tập 2 CD: Cho hình bình hành ABCD. Một đường thẳng đi qua D lần lượt cắt đoạn thẳng BC và tia AB tại M và N sao cho điểm M nằm giữa hai điểm B và C. Chứng minh:
a) $\triangle$NBM $\sim $ $\triangle$NAD;
b) $\triangle$NBM $\sim $ $\triangle$DCM;
c) $\triangle$NAD $\sim $ $\triangle$DCM.
a) Ta có: AD // BC (ABCD là hình bình hành) mà M thuộc BC nên BM // AD
Suy ra: $\triangle$NBM $\sim $ $\triangle$NAD.
b) Ta có: AB // CD (ABCD là hình bình hành) mà N thuộc AB nên BN // CD
Suy ra: $\triangle$NBM $\sim $ $\triangle$DCM.
c) Ta có: $\triangle$NBM $\sim $ $\triangle$NAD (câu a) và $\triangle$NBM $\sim $ $\triangle$DCM (câu b)
Do đó: $\triangle$NAD $\sim $ $\triangle$DCM.
Xem toàn bộ: Giải toán 8 Cánh diều bài 5 Tam giác đồng dạng
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 8 cánh diều
Giải SBT lớp 8 kết nối tri thức
Giải SBT lớp 8 chân trời sáng tạo
Soạn SBT lớp 8 cánh diều
Trắc nghiệm 8 Kết nối tri thức
Trắc nghiệm 8 Chân trời sáng tạo
Trắc nghiệm 8 Cánh diều
Bộ đề thi, đề kiểm tra lớp 8 chân trời sáng tạo
Giáo án lớp 8
Bình luận