Giải Bài tập 6 trang 67 sgk Toán 8 tập 1 Chân trời
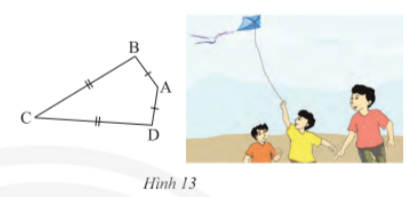
Bài tập 6 trang 67 sgk Toán 8 tập 1 CTST: Ta có tứ giác ABCD với AB = AD, CB = CD (Hình 13) là hình "cái diều".
a) Chứng minh rằng AC là đường trung trực của BD
b) Cho biết $\widehat{B}=95^{\circ},\widehat{C}=35^{\circ}$. Tính $\widehat{A}$ và $\widehat{D}$
a) Ta có: AB = AD (gt) => A thuộc đường trung trực của BD
CB = CD (gt) => C thuộc đường trung trực của BD.
Vậy AC là đường trung trực của BD.
b) Xét ∆ ABC và ∆ADC có:
AB = AD (gt)
CB = CD (gt)
AC chung
nên ∆ ABC = ∆ADC (c.c.c)
Suy ra $\widehat{B}=\widehat{D}=95^{\circ}$
Ta có: $\widehat{A}=360^{\circ}-(95^{\circ}+95^{\circ}+35^{\circ})=135^{\circ}$
Xem toàn bộ: Giải toán 8 chân trời bài 2 Tứ giác
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 8 cánh diều
Giải SBT lớp 8 kết nối tri thức
Giải SBT lớp 8 chân trời sáng tạo
Soạn SBT lớp 8 cánh diều
Trắc nghiệm 8 Kết nối tri thức
Trắc nghiệm 8 Chân trời sáng tạo
Trắc nghiệm 8 Cánh diều
Bộ đề thi, đề kiểm tra lớp 8 chân trời sáng tạo
Giáo án lớp 8
Bình luận