Giải bài tập 4.5 trang 47 SBT toán 10 tập 1 kết nối
Bài tập 4.5. Cho tam giác ABC không vuông, với trực tâm H, nội tiếp đường tròn (O). Kẻ đường kính AA' của đường tròn (O).
a) Chứng minh rằng $\overrightarrow{BH} = \overrightarrow{A'C}$.
b) Gọi M là trung điểm cạnh BC. Tìm mối quan hệ về phương, hướng và độ dài của hai vectơ $\overrightarrow{AH}$ và $\overrightarrow{OM}$.
Trả lời:
a) Do AA' là đường kính của (O) nên $\widehat{ABA'} = \widehat{ACA'} = 90^{o}$
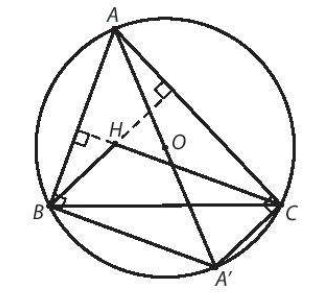
Suy ra A'C $\perp$ AC, A'B $\perp$ AB
H là trực tâm của tam giác ABC ta có: BH $\perp$ AC và CH $\perp$ AB
Từ đó tứ giác BHCA' là hình bình hành
b) Do AA' là đường kính của (O) nên O là trung điểm của AA'
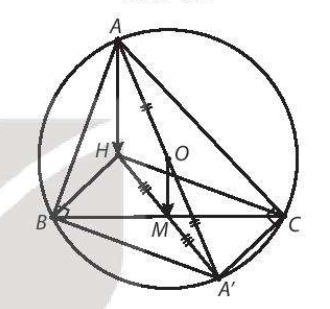
Bởi vì BHCA' là hình bình hành, nên trung điểm M của BC cũng là trung điểm của HA'
Suy ra OM là đường trung bình của tam giác AHA'
Nên OM // AH và OM = $\frac{1}{2}$AH
Như vậy $\overrightarrow{AH}$ và $\overrightarrow{OM}$ cùng hướng và |$\overrightarrow{AH}$| =2|$\overrightarrow{OM}$|
Xem toàn bộ: Giải SBT toán 10 kết nối bài 7 Các khái niệm mở đầu

Bình luận