Giải bài tập 4.4 trang 47 SBT toán 10 tập 1 kết nối
Bài tập 4.4. Cho lục giác đều ABCDEF có tâm O. Xét các vectơ có hai điểm mút lấy từ các điểm O, A, B, C, D, E, F.
a) Hãy chỉ ra các vectơ khác vectơ - không và cùng phương với vectơ $\overrightarrow{OA}$.
b) Tìm các vectơ bằng vectơ $\overrightarrow{AB}$.
Trả lời:
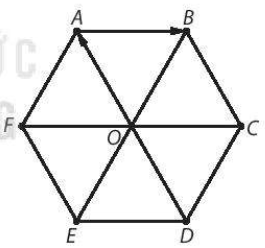
Do ABCDEF là lục giác đều tâm O nên:
- Các cặp cạnh đối diện AB và ED, BC và EF, CD và FA song song và bằng nhau;
- Ba đường chéo chính AD, BE, CF đồng quy tại trung điểm của mỗi đường;
- Mỗi đường chéo chinh song song với một cặp cạnh có đầu mút không thuộc đường chéo ấy.
Suy ra:
a) Các vectơ khác $\overrightarrow{0}$, cùng phương với $\overrightarrow{OA}$ là: $\overrightarrow{OA}$, $\overrightarrow{AO}$, $\overrightarrow{OD}$, $\overrightarrow{DO}$, $\overrightarrow{BC}$, $\overrightarrow{CB}$, $\overrightarrow{EF}$, $\overrightarrow{FE}$, $\overrightarrow{AD}$, $\overrightarrow{DA}$
b) Các vectơ bằng vectơ $\overrightarrow{AB}$ là: $\overrightarrow{AB}$, $\overrightarrow{FO}$, $\overrightarrow{OC}$, $\overrightarrow{AD}$
Xem toàn bộ: Giải SBT toán 10 kết nối bài 7 Các khái niệm mở đầu

Bình luận