Giải bài tập 4 trang 65 sgk Toán 8 tập 2 CD
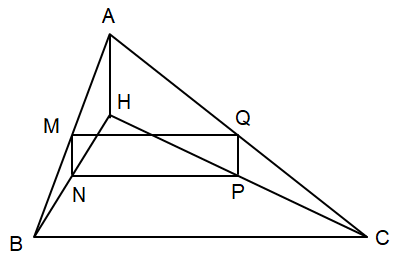
Bài tập 4 trang 65 sgk Toán 8 tập 2 CD: Cho tam giác ABC nhọn có H là trực tâm. Gọi M, N, P, Q lần lượt là trung điểm của các đoạn thẳng AB, BH, HC, CA. Chứng minh tứ giác MNPQ là hình chữ nhật.
Tam giác ABH có: M, N lần lượt là trung điểm của AB, BH.
Suy ra: MN là đường trung bình nên MN // AH và MN = $\frac{1}{2}$AH (1)
Tam giác ACH có: P, Q lần lượt là trung điểm của CH, AC.
Suy ra: PQ là đường trung bình nên PQ // AH và PQ = $\frac{1}{2}$AH (2)
Từ (1)(2) suy ra: MN // PQ và MN = PQ.
Do đó: MNPQ là hình bình hành (3)
Ta có: MN // AH
Mà AH $\perp $ BC (H là trực tâm tam giác ABC)
Suy ra: MN $\perp $ BC
Mà MQ // BC (MQ là đường trung bình của tam giác ABC)
Do đó: MN $\perp $ MQ (4)
Từ (3)(4) suy ra: MNPQ là hình chữ nhật.

Bình luận