Giải bài tập 2 trang 65 sgk Toán 8 tập 2 CD
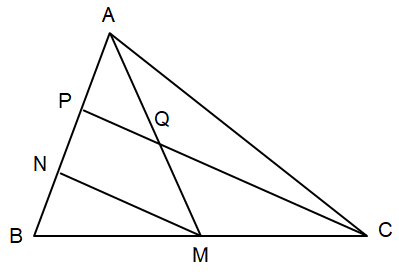
Bài tập 2 trang 65 sgk Toán 8 tập 2 CD: Cho tam giác ABC có AM là đường trung tuyến, các điểm N, P phân biệt thuộc cạnh AB sao cho AP = PN = NB. Gọi Q là giao điểm của AM và CP. Chứng minh:
a) MN // CP;
b) AQ = QM;
c) CP = 4PQ.
a) Tam giác BCP có: PN = NB; BM = MC (M là trung điểm của BC)
Suy ra: $\frac{BN}{NP}=\frac{BM}{MC}$
Do đó: MN // CP (Định lí Thalès).
b) Tam giác AMN có: MN // PQ (MN // CP, Q $\in $ CP)
Suy ra: $\frac{AP}{PN}=\frac{AQ}{QM}$
Mà AP = PN
Do đó: AQ = QM.
c) Do MN // PQ nên $\frac{PQ}{NM}=\frac{AP}{AN}$
Mà AP = $\frac{1}{2}$AN
Suy ra: PQ = $\frac{1}{2}$NM. (1)
Do MN // CP nên $\frac{NM}{CP}=\frac{BN}{BP}$
Mà BN = $\frac{1}{2}$BP
Suy ra: NM = $\frac{1}{2}$CP. (2)
Từ (1)(2) suy ra: PQ = $\frac{1}{2}$.$\frac{1}{2}$CP = $\frac{1}{4}$CP hay CP = 4PQ.

Bình luận