Giải bài tập 26 trang 73 SBT toán 7 tập 2 cánh diều
Bài 26. Cho $\Delta ABC=\Delta MNP.$ Hai tia phân giác của góc B và C cắt nhau tại O tạo thành góc BOC bằng 120$^{\circ}$. Tính tổng số đo các góc MNP và MPN của tam giác MNP.
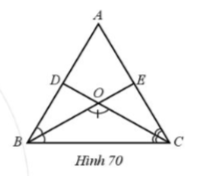
$\widehat{BOC}=180^{\circ}-(\widehat{OBC}+\widehat{OCB})=180^{\circ}-(\frac{\widehat{ABC}}{2}+\frac{\widehat{ACB}}{2})$
Mà $\widehat{BOC}=120^{\circ}$ nên $\widehat{ABC}+\widehat{ACB}=120$ (1)
Do $\Delta ABC=\Delta MNP$ nên:
$\widehat{ABC}=\widehat{MNP}$ và $\widehat{ACB}=\widehat{MPN}$
hay $\widehat{ABC}+\widehat{ACB}=\widehat{MNP}+\widehat{MPN}$ (2)
Từ (1) và 92), ta có $\widehat{MNP}+\widehat{MPN}=120^{\circ}$
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 7 cánh diều
Giải SBT lớp 7 kết nối tri thức
Giải SBT lớp 7 chân trời sáng tạo
Giải SBT lớp 7 cánh diều
Trắc nghiệm 7 Kết nối tri thức
Trắc nghiệm 7 Chân trời sáng tạo
Trắc nghiệm 7 Cánh diêu
Bình luận