Giải bài 3 trang 75 toán 7 tập 1 chân trời sáng tạo
Bài 3 trang 75 toán 7 tập 1 CTST
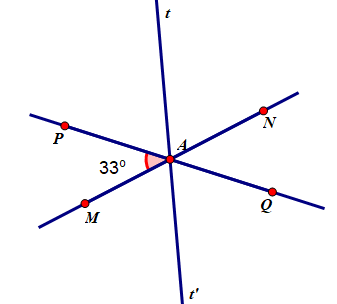
Cho đường thẳng MN, PQ cắt nhau tại A và tạọ thành $\widehat{PAM}$ = 33o ( Hình 9)

a) Tính số đo các góc còn lại.
b) Vẽ tia At là tia phân giác của$\widehat{PAN}$. Hãy tính số đo của $\widehat{tAQ}$. Vẽ At’ là tia đối của tia At. Giải thích tại sao At’ là tia phân giác của $\widehat{MAQ}$.
a) Ta có:
$\widehat{POM}$= $\widehat{QAN}$ ( 2 góc đối đỉnh)
mà $\widehat{POM}$= 33o
=> $\widehat{QAN}$= 33o
Vì $\widehat{PAN}$ + $\widehat{PAM}$ = 180o ( 2 góc kề bù)
=> $\widehat{PAN}$ + 33o = 180o (2 góc kề bù)
=> $\widehat{PAN}$ = 180o - 33o = 147o
Vì $\widehat{PAN}$ = $\widehat{QAM}$ (2 góc đối đỉnh)
mà $\widehat{PAN}$ = 157o
=> $\widehat{QAM}$= 157o
b)
Vì At là tia phân giác của $\widehat{PAN}$
=> $\widehat{PAt}$= $\widehat{tAN}$ = $\frac{1}{2}$. $\widehat{PAN}$ = $\frac{1}{2}$. 157o= 78,5o
Vì $\widehat{tAQ}$ + $\widehat{PAt}$ = 180o (2 góc kề bù)
=> $\widehat{tAQ}$ + 78,5o = 180o => $\widehat{tAQ}$ = 180o - 78,5o = 101,5o
Vẽ At’ là tia đối của tia At, ta được $\widehat{QAt'}$ = $\widehat{PAt}$ ( 2 góc đối đỉnh)
Ta có: $\widehat{QAt'}$ = $\widehat{MAt'}$ = $\frac{1}{2}$. $\widehat{MAQ}$
=> At' là tia phân giác của $\widehat{MAQ}$.
Xem toàn bộ: Giải bài 2 Tia phân giác

Bình luận