Bài tập file word mức độ vận dụng cao bài 17: Tính chất đường phân giác của tam giác

Câu 1: 

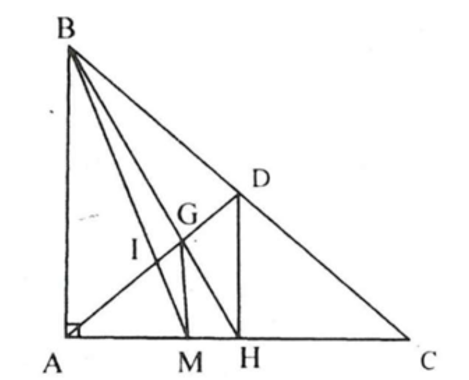
DADH có: GM//DH $\Rightarrow \frac{AM}{AH}=\frac{AG}{AD}=\frac{2}{3}\Rightarrow 3AM=2.AH=AC=AM+MC$

Hay MC  = 2AM

Áp dụng tính chất đường phân giác trong DABC, ta có:

$\Rightarrow \frac{AM}{AH}=\frac{AG}{AD}=\frac{2}{3}\Rightarrow 3AM=2.AH=AC=AM+MC$

Vậy DABD cân tại B nên BI vừa là phân giác vừa là đường cao. Do đó BM $\perp $AD

Câu 2.

Áp dụng tính chất đường phân giác trong và ngoài của tam giác, ta có:

$\frac{BD}{ID}=\frac{BF}{IF};\frac{CE}{IE}=\frac{CD}{ID};\frac{AF}{IF}=\frac{AE}{IE}$

Ta có: $\frac{BC}{ID}=\frac{BD}{ID}-\frac{CD}{ID}=\frac{BF}{IF}-\frac{CE}{IE}(1)$

Ta có: $\frac{AC}{IE}=\frac{AE}{IE}+\frac{CE}{IE}=\frac{AF}{IF}+\frac{CE}{IE}(1)$

Từ (1) và (2) cộng vế với vế, suy ra:

$\frac{BC}{ID}+\frac{AC}{IE}=\frac{BF}{IF}+\frac{AF}{IF}=\frac{AB}{IF}$