Bài tập file word mức độ nhận biết bài 17: Tính chất đường phân giác của tam giác
1. NHẬN BIẾT (7 câu)
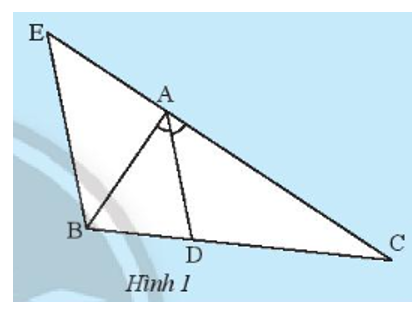
Câu 1: Cho tam giác ABC có đường phân giác AD. Vẽ đường thẳng qua B song song với AD và cắt đường thẳng AC tại E (Hình 1). Hãy giải thích tại sao:
a) tam giác BAE cân tại A
b) $\frac{DB}{DC}=\frac{AE}{AC}=\frac{AB}{AC}$
Câu 2: Tính độ dài cạnh MQ của tam giác MPQ trong Hình 6

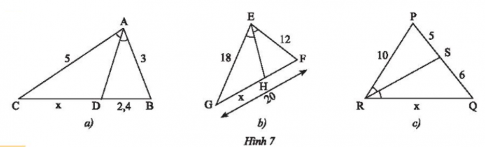
Câu 3: Tính độ dài x trong Hình 7
Câu 4: Tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 10 cm. Đường phân giác của góc BAC cắt cạnh BC tại D
a) Tính độ dài các đoạn thẳng DB và DC
b) Tính tỉ số diện tích giữa ΔADBvà ΔADC
Câu 5. Cho tam giác ABC có AB cm BC = 5,7 cm và CA = 6cm . Tia phân giác của góc BAC cắt cạnh BC ở E . Tính các đoạn EB, EC
Câu 6. Cho tam giác ABC có BC cm AC AB = = 24 , 3 . Tia phân giác của góc ngoài tại A cắt đường thẳng BC ở E . Tính độ dài EB .
Câu 1:
a) Ta có: BE // AD suy ra $\widehat{AEB}=\widehat{CAD}$ (hai góc đồng vị), $\widehat{ABE}=\widehat{BAD}$ (hai góc so le trong)
AD là tia phân giác góc $\widehat{BAC}$ nên BADˆ=CADˆ
Do đó: $\widehat{AEB}=\widehat{ABE}$
suy ra tam giác BAE cân tại A
b) Xét tam giác BCE có AD // BE, theo định lí Thales ta có:
$\frac{DB}{DC}=\frac{AE}{AC}$
Mà AE = AB (do tam giác ABE cân tại A)
Do đó: $\frac{DB}{DC}=\frac{AE}{AC}=\frac{AB}{AC}$
Câu 2:
Trong tam giác MPQ , ta có MN là đường phân giác góc M, suy ra $\frac{NP}{NQ}=\frac{MP}{MQ}$
nên $\frac{4}{5}=\frac{7}{MQ}$
Suy ra $MQ=\frac{7\times 5}{4}=8,75$
Câu 3:
a) Trong tam giác ABC , ta có AD là đường phân giác góc A, suy ra $\frac{DC}{DB}=\frac{AC}{AB}$ nên $\frac{x}{2,4}=\frac{5}{3}$
Suy ra $x=\frac{5\times 2,4}{3}=4$
b) Trong tam giác EFG , ta có EH là đường phân giác góc E, suy ra $\frac{HG}{HF}=\frac{EG}{EF}$ nên $\frac{HG}{HF}=\frac{EG}{EF}$
Suy ra 12x=18(20−x) ⇒ $x=\frac{18\times 20}{30}=12$
c) Trong tam giác PQR , ta có RS là đường phân giác góc R, suy ra $\frac{SP}{SQ}=\frac{PR}{QR}$ nên $\frac{5}{6}=\frac{10}{x}$
Suy ra $x=\frac{6\times 10}{5}=12$
Câu 4:
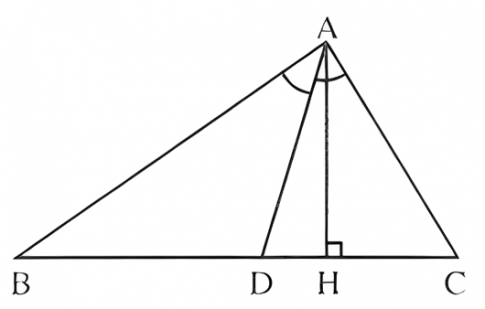
a) Tam giác ABC có AD là đường phân giác
⇒ $\frac{DB}{AB}=\frac{DC}{AC}$
⇒ $\frac{DB}{AB}=\frac{DC}{AC}=\frac{DB+DC}{AB+AC}=\frac{BC}{AB+AC}$
Nên $\frac{DB}{8}=\frac{DC}{6}=\frac{10}{8+6}$
$DB=\frac{40}{7}$ cm, $BC=\frac{30}{7}$ cm
b) Vẽ AH⊥BC tại H
$\frac{S_{ABD}}{S_{ACD}}=\frac{\frac{1}{2}AH.DB}{\frac{1}{2}AH.DC}$
$=\frac{DB}{DC}=\frac{\frac{40}{7}}{\frac{30}{7}}=\frac{4}{3}$
Câu 5.
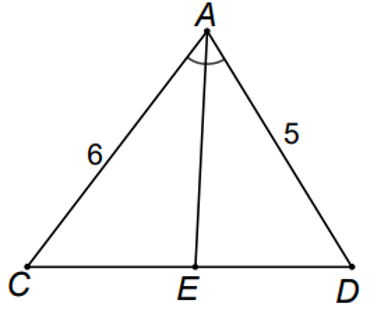
Áp dụng tính chất của đường phân giác AD vào tam giác ABC và tính chất của dãy tỉ số bằng nhau, ta có:
$\frac{EB}{BA}=\frac{EC}{CA}=\frac{EB+EC}{BA+CA}=\frac{BC}{BA+CA}$
Hay $\frac{EB}{5}=\frac{EC}{6}=\frac{7}{11}$
=> $EB=\frac{35}{11}$(cm); $EC=\frac{42}{11}$(cm)
Câu 6.
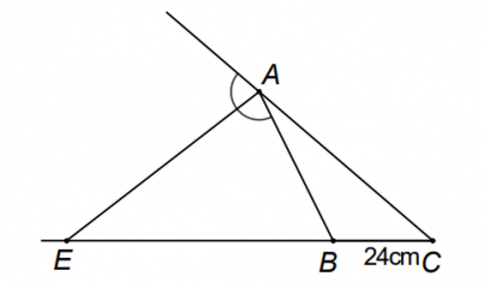
Áp dụng tính chất của đường phân giác ngoài AE vào tam giác ABC , ta được:
$\frac{EB}{EC}=\frac{BA}{CA}=\frac{BA}{3BA}=\frac{1}{3}$
$\Rightarrow \frac{EB}{1}=\frac{EC}{3}$
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
$\frac{EB}{1}=\frac{EC}{3}=\frac{EC-EB}{3-1}=\frac{BC}{2}=\frac{24}{2}=12$
Vậy EB =12 cm

Bình luận