Câu hỏi tự luận mức độ vận dụng Toán 9 ctst bài 1: Căn bậc hai
3. VẬN DỤNG (8 câu)
Câu 1: Đại Kim tự tháp Giza là Kim tự tháp Ai Cập lớn nhất và là lăng mộ của Vương triều thứ Tư của pharaoh Khufu. Nền kim tự tháp có dạng hình vuông với diện tích khoảng 53 052 m2. Hỏi độ dài cạnh của nền kim tự tháp đó là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
Câu 2: Giông bão thổi mạnh, một cây bị gãy gập xuống làm ngọn cây chạm đất và tạo với phương nằm ngang một góc 45° (minh họa ở hình vẽ). Người ta đo được khoảng cách từ chỗ ngọn cây chạm đất đến gốc cây là 4,5 m. Giả sử cây mọc vuông góc với mặt đất, hãy tính chiều cao của cây đó theo đơn vị mét (làm tròn kết quả đến hàng phần mười).
Câu 3: Trong Vật lí, quãng đường S (tính bằng mét) của một vật rơi tự do được cho bởi công thức ![]() , trong đó t là thời gian rơi (tính bằng giây). Hỏi sau bao nhiêu giây thì vật sẽ chạm đất nếu được thả rơi tự do từ độ cao 122,5 mét?
, trong đó t là thời gian rơi (tính bằng giây). Hỏi sau bao nhiêu giây thì vật sẽ chạm đất nếu được thả rơi tự do từ độ cao 122,5 mét?
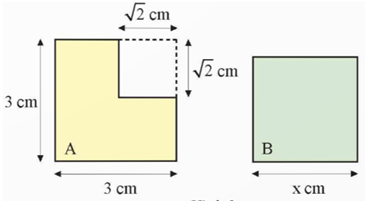
Câu 4: Biết rằng hình A và hình vuông B trong hình vẽ dưới có diện tích bằng nhau. Tính độ dài cạnh x của hình vuông B.
Câu 5: Để lái xe an toàn khi đi qua đoạn đường có dạng cung tròn, người lái cần biết tốc độ tối đa cho phép là bao nhiêu. Vì thế, ở những đoạn đường đó thường có bảng chỉ dẫn cho tốc độ tối đa cho phép của ô tô. Tốc độ tối đa cho phép v (m/s) được tính bởi công thức ![]() , trong đó r (m) là bán kính của cung đường, g = 9,8 m/s2, μ là hệ số ma sát trượt của đường.
, trong đó r (m) là bán kính của cung đường, g = 9,8 m/s2, μ là hệ số ma sát trượt của đường.
a) Hãy viết biểu thức tính v theo r khi biết ![]() .
.
b) Trong toán học, biểu thức đó được gọi là gì?
Câu 6: Một chiếc thang dài 5 m tựa vào bức tường như hình vẽ.
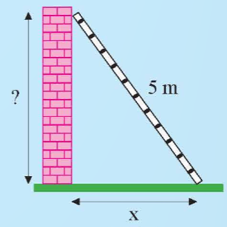
a) Nếu chân thang cách chân tường x (m) thì đỉnh thang ở độ cao bao nhiêu so với chân tường?
b) Tính độ cao trên khi x nhận giá trị lần lượt là 1; 2; 3; 4.
Câu 7: Sóng thần (tsunami) là một loạt các đợt sóng tạo nên khi một thể tích lớn của nước đại dương bị dịch chuyển chớp nhoáng trên một quy mô lớn. Động đất cùng những dịch chuyển địa chất lớn bên trên hoặc bên dưới mặt nước, núi lửa phun và va chạm thiên thạch đều có khả năng gây ra sóng thần. Cơn sóng thần khởi phát từ dưới đáy biển sâu, khi còn ngoài xa khơi, sóng có biên độ (chiều cao sóng) khá nhỏ nhưng chiều dài của cơn sóng lên đến hàng trăm km. Con sóng đi qua đại dương với tốc độ trung bình 500 dặm một giờ. Khi tiến tới đất liền, đáy biển trở nên nông, con sóng không còn dịch chuyển nhanh được nữa, vì thế nó bắt đầu “dựng đứng lên” có thể đạt chiều cao một tòa nhà sáu tầng hay hơn nữa và tàn phá khủng khiếp.
Tốc độ của con sóng thần và chiều sâu của đại dương liên hệ bởi công thức ![]() . Trong đó,
. Trong đó, ![]() , d (deep) là chiều sâu đại dương tính bằng m, s là vận tốc của sóng thần tính bằng m/s.
, d (deep) là chiều sâu đại dương tính bằng m, s là vận tốc của sóng thần tính bằng m/s.

a) Biết độ sâu trung bình của đại dương trên trái đất là d = 3790 mét hãy tính tốc độ trung bình của các con sóng thần xuất phát từ đáy các đại dương theo km/h.
b) Susan Kieffer, một chuyên gia về cơ học chất lỏng địa chất của đại học Illinois tại Mỹ, đã nghiên cứu năng lượng của trận sóng thần Tohoku 2011 tại Nhật Bản. Những tính toán của Kieffer cho thấy tốc độ sóng thần vào xấp xỉ 220 m/giây. Hãy tính độ sâu của đại dương nơi xuất phát con sóng thần này.
Câu 8: Vận tốc v (m/s ) của một tàu lượn di chuyển trên một cung tròn có bán kính r(m) được cho bởi công thức: ![]() . Trong đó a là gia tốc của tàu (m/s2) (gia tốc là đại lượng vật lý đặc trưng cho sự thay đổi của vận tốc theo thời gian. Nó là một trong những đại lượng cơ bản dùng để mô tả chuyển động và là độ biến thiên của vận tốc theo thời gian).
. Trong đó a là gia tốc của tàu (m/s2) (gia tốc là đại lượng vật lý đặc trưng cho sự thay đổi của vận tốc theo thời gian. Nó là một trong những đại lượng cơ bản dùng để mô tả chuyển động và là độ biến thiên của vận tốc theo thời gian).

a) Nếu tàu lượn đang chạy với vận tốc v = 14m/s và muốn đạt mức gia tốc tối đa cho phép là ![]() thì bán kính tối thiểu của cung tròn phải là bao nhiêu để xe không văng ra khỏi đường ray?
thì bán kính tối thiểu của cung tròn phải là bao nhiêu để xe không văng ra khỏi đường ray?
b) Nếu tàu lượn đang di chuyển với vận tốc v = 8m/s xung quanh một cung tròn có bán kính r = 25m thì có gia tốc tối đa cho phép là bao nhiêu?
Câu 1:
Gọi a (m) là độ dài cạnh của nền kim tự tháp dạng hình vuông (a > 0).
Diện tích của nền kim tự tháp đó là a2 (m2).
Theo bài, ta có: a2 = 53 052, suy ra ![]() (m).
(m).
Câu 2:
Giả sử hình ảnh của cây được mô tả như hình vẽ dưới đây:
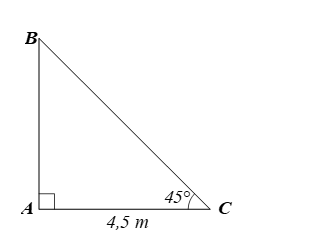
Vì ∆ABC vuông cân tại A có ![]() nên ∆ABC vuông cân tại A.
nên ∆ABC vuông cân tại A.
Do đó AB = AC = 4,5 m.
Áp dụng định lí Pythagore vào ∆ABC vuông cân tại A, ta có: BC2 = AB2 + AC2
Suy ra ![]() (m).
(m).
Câu 3:
Quãng đường vật rơi tự do từ độ cao 122,5 mét đến khi chạm đất là S = 122,5 mét.
Từ công thức S = 4,9t2, nên ![]() (giây) (do t > 0).
(giây) (do t > 0).
Suy ra ![]() (giây).
(giây).
Câu 4:
• Xét hình A:
Diện tích cả hình vuông cạnh 3 cm là: 3 . 3 = 9 (cm2).
Diện tích cả hình vuông cạnh ![]() là:
là: ![]()
Do đó, diện tích hình A là: 9 – 2 = 7 (cm2).
• Xét hình B:
Hình vuông B bằng diện tích hình A là 7 cm2.
Do đó ![]() suy ra
suy ra ![]() .
.
Câu 5:
a) Theo bài, g = 9,8 m/s2 và μ = 0,12.
Thay vào biểu thức ![]() , ta được:
, ta được: ![]() (m/s).
(m/s).
Vậy biểu thức tính v theo r là ![]() (m/s).
(m/s).
b) Trong toán học, biểu thứ trên được gọi là căn thức bậc hai.
Câu 6:
a) Gọi tam giác ABC như hình vẽ.
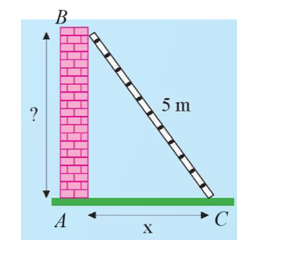
a) Trong thực tế bức tường vuông góc với mặt đất nên AB ⊥ AC.
Xét tam giác ABC vuông tại A, áp dụng định lí Pythagore, ta có:
BC2 = AB2 + AC2
Suy ra AC2 = BC2 – AB2 = 52 – x2 = 25 – x2.
Do đó ![]() (m).
(m).
Vậy nếu chân thang cách chân tường x (m) thì đỉnh thang ở độ cao ![]() (m) so với chân tường.
(m) so với chân tường.
b)
- Khi ![]() thì độ cao đỉnh thang so với chân tường là:
thì độ cao đỉnh thang so với chân tường là: ![]()
- Khi ![]() thì độ cao đỉnh thang so với chân tường là:
thì độ cao đỉnh thang so với chân tường là: ![]()
- Khi ![]() thì độ cao đỉnh thang so với chân tường là:
thì độ cao đỉnh thang so với chân tường là: ![]()
- Khi ![]() thì độ cao đỉnh thang so với chân tường là:
thì độ cao đỉnh thang so với chân tường là: ![]()
Vậy x nhận giá trị lần lượt là 1; 2; 3; 4. thì độ cao đỉnh thang so với chân tường lần lượt là ![]()
Câu 7:
a) Thay ![]() vào công thức
vào công thức ![]() , ta được:
, ta được:
![]()
Vậy tốc độ trung bình của các con sóng thần là 193m/s
b) Thay s = 220; g = 9,81 vào công thức ![]() , ta được:
, ta được:
![]()
Câu 8:
a) Thay ![]() vào công thức
vào công thức ![]() , ta được:
, ta được:
![]()
Vậy bán kính tối thiểu của cung tròn phải là 21,8m.
b) Thay ![]() vào công thức
vào công thức ![]() , ta được:
, ta được:
![]()
Vậy gia tốc tối đa cho phép là 2,56m/s2
Xem toàn bộ: Câu hỏi tự luận Toán 9 Chân trời bài 1: Căn bậc hai
Giải những bài tập khác
Giải bài tập những môn khác
Môn học lớp 9 KNTT
5 phút giải toán 9 KNTT
5 phút soạn bài văn 9 KNTT
Văn mẫu 9 kết nối tri thức
5 phút giải KHTN 9 KNTT
5 phút giải lịch sử 9 KNTT
5 phút giải địa lí 9 KNTT
5 phút giải hướng nghiệp 9 KNTT
5 phút giải lắp mạng điện 9 KNTT
5 phút giải trồng trọt 9 KNTT
5 phút giải CN thực phẩm 9 KNTT
5 phút giải tin học 9 KNTT
5 phút giải GDCD 9 KNTT
5 phút giải HĐTN 9 KNTT
Môn học lớp 9 CTST
5 phút giải toán 9 CTST
5 phút soạn bài văn 9 CTST
Văn mẫu 9 chân trời sáng tạo
5 phút giải KHTN 9 CTST
5 phút giải lịch sử 9 CTST
5 phút giải địa lí 9 CTST
5 phút giải hướng nghiệp 9 CTST
5 phút giải lắp mạng điện 9 CTST
5 phút giải cắt may 9 CTST
5 phút giải nông nghiệp 9 CTST
5 phút giải tin học 9 CTST
5 phút giải GDCD 9 CTST
5 phút giải HĐTN 9 bản 1 CTST
5 phút giải HĐTN 9 bản 2 CTST
Môn học lớp 9 cánh diều
5 phút giải toán 9 CD
5 phút soạn bài văn 9 CD
Văn mẫu 9 cánh diều
5 phút giải KHTN 9 CD
5 phút giải lịch sử 9 CD
5 phút giải địa lí 9 CD
5 phút giải hướng nghiệp 9 CD
5 phút giải lắp mạng điện 9 CD
5 phút giải trồng trọt 9 CD
5 phút giải CN thực phẩm 9 CD
5 phút giải tin học 9 CD
5 phút giải GDCD 9 CD
5 phút giải HĐTN 9 CD
Trắc nghiệm 9 Kết nối tri thức
Trắc nghiệm 9 Chân trời sáng tạo
Trắc nghiệm 9 Cánh diều
Tài liệu lớp 9
Văn mẫu lớp 9
Đề thi lên 10 Toán
Đề thi môn Hóa 9
Đề thi môn Địa lớp 9
Đề thi môn vật lí 9
Tập bản đồ địa lí 9
Ôn toán 9 lên 10
Ôn Ngữ văn 9 lên 10
Ôn Tiếng Anh 9 lên 10
Đề thi lên 10 chuyên Toán
Chuyên đề ôn tập Hóa 9
Chuyên đề ôn tập Sử lớp 9
Chuyên đề toán 9
Chuyên đề Địa Lý 9
Phát triển năng lực toán 9 tập 1
Bài tập phát triển năng lực toán 9

Bình luận