Câu hỏi tự luận mức độ vận dụng Toán 12 cd Bài 2: Công thức xác suất toàn phần. Công thức Bayes
3. VẬN DỤNG (8 câu)
Câu 1: Tại một địa phương có 500 người cao tuổi, bao gồm 260 nam và 240 nữ. Trong nhóm người cao tuổi nam và nữ lần lượt có 40% và 55% bị bệnh tiểu đường. Chọn ngẫu nhiên một người. Xác suất để chọn được một người không bị bệnh tiểu đường là bao nhiêu?
Câu 2: Năm 2001, Cộng đồng châu Âu có làm một đợt kiểm tra rất rộng rãi các con bò để phát hiện những con bị bệnh bò điên. Không có xét nghiệm nào cho kết quả chính xác 100%. Một loại xét nghiệm, mà ở đây ta gọi là xét nghiệm A, cho kết quả như sau: Khi con bò bị bệnh bò điên thì xác suất để có phản ứng dương tính trong xét nghiệm A là 70%, còn khi con bò không bị bệnh thì xác suất để có phản ứng dương tính trong xét nghiệm A là 10%. Biết rằng tỉ lệ bò bị mắc bệnh bò điên ở Hà Lan là 13 con trên 1 000 000 con (Nguồn: F. M. Dekking et al., A modern introduction to probability and statistics – Understanding why and how, Springer, 2005). Hỏi khi một con bò ở Hà Lan có phản ứng dương tính với xét nghiệm A thì xác suất để nó bị mắc bệnh bò điên là bao nhiêu?
Câu 3: Một xí nghiệp mỗi ngày sản xuất ra 1 600 sản phẩm, trong đó có 35 sản phẩm lỗi. Lần lượt lấy ra ngẫu nhiên 2 sản phẩm không hoàn lại để kiểm tra. Tính xác suất của các biến cố:
A: “Sản phẩm lấy ra lần thứ hai không bị lỗi, biết sản phẩm lấy ra lần thứ nhất không bị lỗi”;
B: “Sản phẩm lấy ra lần thứ hai bị lỗi, biết sản phẩm lấy ra lần thứ nhất không bị lỗi”;
C: “Sản phẩm lấy ra lần thứ hai không bị lỗi, biết sản phẩm lấy ra lần thứ nhất bị lỗi”;
D: “Sản phẩm lấy ra lần thứ hai bị lỗi, biết sản phẩm lấy ra lần thứ nhất bị lỗi”; E: “Sản phẩm lấy ra lần thứ hai bị lỗi”.
Câu 4: Thực hiện khảo sát tại một địa phương mà số trẻ em nam gấp 1,5 lần số trẻ em nữ, có 8% số trẻ em nam bị hen phế quản, 5% số trẻ em nữ bị hen phế quản. Chọn ngẫu nhiên 1 trẻ em. Giả sử trẻ em được chọn bị hen phế quản. Xác suất chọn được trẻ em nam là bao nhiêu (làm tròn kết quả đến hàng phần mười)?
Câu 5: Trường Bình Phúc có 20% học sinh tham gia câu lạc bộ âm nhạc, trong số học sinh đó có 85% học sinh biết chơi đàn guitar. Ngoài ra, có 10% số học sinh không tham gia câu lạc bộ âm nhạc cũng biết chơi đàn guitar. Chọn ngẫu nhiên 1 học sinh của trường. Giả sử học sinh đó biết chơi đàn guitar. Xác suất chọn được học sinh thuộc câu lạc bộ âm nhạc là bao nhiêu?
Câu 6: Một khu dân cư có 60% các hộ gia đình có không quá 4 thành viên. Trong các gia đình có không quá 4 thành viên, có 20% gia đình có ba thế hệ cùng chung sống; trong các gia đình có trên 4 thành viên, có 70% gia đình có ba thế hệ cùng chung sống. Chọn ngẫu nhiên 1 hộ gia đình trong khu dân cư. Biết rằng gia đình đó có ba thế hệ cùng chung sống, tính xác suất để gia đình đó có trên 4 thành viên.
Câu 7: Một xưởng máy sử dụng một loại linh kiện được sản xuất từ hai cơ sở I và II. Số linh kiện do cơ sở I sản xuất chiếm 61%, số linh kiện do cơ sở II sản xuất chiếm 39%. Tỉ lệ linh kiện đạt tiêu chuẩn của cơ sở I, cơ sở II lần lượt là 93%, 82%. Kiểm tra ngẫu nhiên 1 linh kiện ở xưởng máy.
Xét các biến cố:
![]() : “Linh kiện được kiểm tra do cơ sở I sản xuất”;
: “Linh kiện được kiểm tra do cơ sở I sản xuất”;
![]() : “Linh kiện được kiểm tra do cơ sở II sản xuất”;
: “Linh kiện được kiểm tra do cơ sở II sản xuất”;
![]() : “Linh kiện được kiểm tra đạt tiêu chuẩn”.
: “Linh kiện được kiểm tra đạt tiêu chuẩn”.
Tính xác suất để linh kiện được kiểm tra đạt tiêu chuẩn và xác suất để linh kiện được kiểm tra do cơ sở I sản xuất biết rằng linh kiện đó đạt tiêu chuẩn.
Câu 8: Một kho hàng có 85% sản phẩm loại I và 15% sản phẩm loại II, trong đó có 1% sản phẩm loại I bị hỏng, 4% sản phẩm loại II bị hỏng. Các sản phẩm có kích thước và hình dạng như nhau. Một khách hàng chọn ngẫu nhiên 1 sản phẩm. Xét các biến cố:
A: “Khách hàng chọn được sản phẩm loại I”;
B: “Khách hàng chọn được sản phẩm không bị hỏng”.
Tính xác suất để khách hàng chọn được sản phẩm không bị hỏng và xác suất để khách hàng chọn được sản phẩm loại I biết rằng sản phẩm đó không bị hỏng.
Câu 1:
Xét các biến cố:
![]() : “Chọn được người không bị bệnh tiểu đường”;
: “Chọn được người không bị bệnh tiểu đường”;
![]() : “Chọn được người cao tuổi là nam”;
: “Chọn được người cao tuổi là nam”;
![]() : “Chọn được người cao tuổi là nữ”.
: “Chọn được người cao tuổi là nữ”.
Từ giả thiết, ta có:
![]()
![]()
Theo công thức xác suất toàn phần, ta có:
![]()
Vậy xác suất để chọn được một người không bị bệnh tiểu đường là ![]() .
.
Câu 2:
Xét các biến cố
M: “Con bò ở Hà Lan bị bệnh bò điên”;
D: “Con bò ở Hà Lan có phản ứng dương tính với xét nghiệm A”.
Theo giả thiết, ta có:
![]()
Theo công thức xác suất toàn phần, ta có:
![]()
![]()
Theo công thức Bayes, ta có:
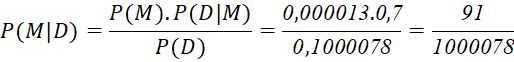
Vậy khi một con bò ở Hà Lan có phản ứng dương tính với xét nghiệm A thì xác suất để nó bị mắc bệnh bò điên là ![]() .
.
Câu 3:
Xét các biến cố:
M: “Sản phẩm lấy ra lần thứ nhất không bị lỗi”;
N: “Sản phẩm lấy ra lần thứ hai không bị lỗi”.
Khi đó, ![]()
![]() .
.
Sau khi lấy một sản phẩm không bị lỗi thì số sản phẩm còn lại 1599, số sản phẩm lỗi là 35 nên xác suất của biến cố A là:
![]()
Xác suất của biến cố B là: ![]()
Sau khi lấy một sản phẩm bị lỗi thì số sản phẩm còn lại 1599, số sản phẩm lỗi là 34 nên xác suất của biến cố C là:
![]()
xác suất của biến cố D là
![]()
Theo công thức xác suất toàn phần, xác suất của biến cố E là:
![]()
![]()
Câu 4:
Xét các biến cố:
A: “Chọn được trẻ em nam”;
B: “Chọn được trẻ em bị hen phế quản”.
Khi đó, ![]()
![]()
Theo công thức xác suất toàn phần, ta có:
![]()
Theo công thức Bayes, xác suất chọn được trẻ em nam, biết trẻ em đó bị hen phế quản là:
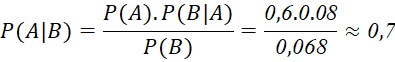
Câu 5:
Xét các biến cố:
A: “Chọn được học sinh thuộc câu lạc bộ âm nhạc”;
B: “Chọn được học sinh biết chơi đàn guitar”.
Khi đó, ![]()
Theo công thức xác suất toàn phần, ta có:
![]()
Theo công thức Bayes, xác suất chọn được học sinh thuộc câu lạc bộ âm nhạc, biết học sinh đó chơi được đàn guitar, là:
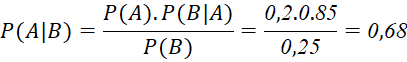
Câu 6:
Gọi M là biến cố “Gia đình có trên 4 thành viên”, N là biến cố “Gia đình có 3 thế hệ chung sống”.
Khi đó, ![]()
Theo công thức xác suất toàn phần, ta có:
![]()
Theo công thức Bayes, xác suất để gia đình đó có trên 4 thành viên, biết rằng gia đình đó có ba thế hệ cùng chung sống là:
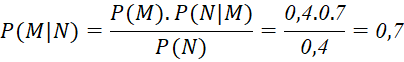
Câu 7:
Theo giả thiết, ta có: ![]() ;
; ![]() .
.
Theo công thức xác suất toàn phần, xác suất để linh kiện được kiểm tra đạt tiêu chuẩn là:
![]()
Theo công thức Bayes, xác suất để linh kiện được kiểm tra do cơ sở I sản xuất biết rằng linh kiện đó đạt tiêu chuẩn là:
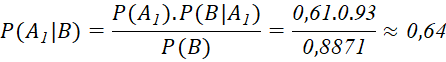
Câu 8:
Theo giả thiết, ta có: ![]()
![]() ;
; ![]() .
.
Theo công thức xác suất toàn phần, xác suất để khách hàng chọn được sản phẩm không bị hỏng là:
![]()
Theo công thức Bayes, xác suất để khách hàng chọn được sản phẩm loại I biết rằng sản phẩm đó không bị hỏng là:
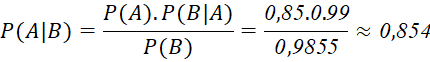
Giải những bài tập khác
Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều

Bình luận