I. TỨ GIÁC

1. Nhận biết tứ giác

HĐ1

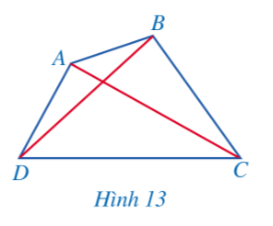
Đáp án (SGK – tr.98).

Nhận xét: Tứ giác có 4 cạnh, 2 đường chéo, 4 đỉnh và 4 góc.

Ghi chú: Trong tứ giác ABCD:

• Hai cạnh kề nhau (chẳng hạn: AB, BC) không cùng thuộc một đường thẳng;
• Không có ba đỉnh nào thẳng hàng;
• Có thể đọc tên góc theo tên đỉnh, chẳng hạn, góc ABC còn gọi là góc B và góc đó còn gọi là góc trong của tứ giác.

2. Nhận biết tứ giác lồi.

HĐ2

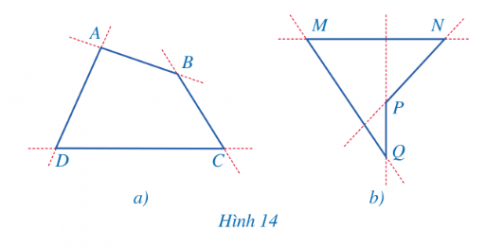
• Hình 14a: Tứ giác ABCD nằm về một phía của đường thẳng chứa một cạnh bất kì của tứ giác đó.
• Hình 14b: Tứ giác MNPQ không nằm về một phía của đường thẳng chứa cạnh NP hoặc cạnh PQ của tứ giác.

Khái niệm: Tứ giác lồi là tứ giác luôn nằm về một phía của đường thẳng chứa một cạnh bất kì của tứ giác đó.

Ví dụ 1: (SGK – tr.99)

Hướng dẫn giải (SGK – tr.99)

Quy ước: Từ nay về sau, khi nói về tứ giác mà không có chú thích gì thêm thì ta hiểu đó là tứ giác lồi.

II. TỔNG CÁC GÓC MỘT TỨ GIÁC

HĐ3

a) Theo định lí tổng ba góc trong một tam giác ta có:

$T_{1}$ là tổng các góc của ∆ABC nên $T_{1}$ = 180°

$T_{2}$ là tổng các góc của ∆ACD nên $T_{2}$ = 180°

Vậy $T_{1}+T_{2}$ = $180^{\circ}$+ $180^{\circ}$ = $360^{\circ}$

b) Ta có: T = $\widehat{ABC}+\widehat{BCD}+\widehat{CDA}+\widehat{DAB}$

mà $\widehat{BCD}$ = $\widehat{BCA}$ + $\widehat{ACD}$ 

$\widehat{DAB}$= $\widehat{DAC}$+$\widehat{BAC}$

Vậy T= $T_{1}+T_{2}$ = $360^{\circ}$

Định lí: Tổng các góc của một tứ giác bằng 360°.

Chẳng hạn, với tứ giác ABCD 

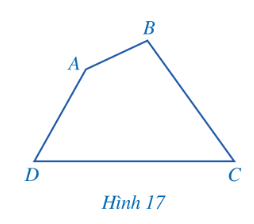
Ta có: $\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^{o}$

Ví dụ 2: (SGK – tr.100)

Hướng dẫn giải (SGK – tr.100).

Luyện tập 

Tổng các góc của một tứ giác bằng 360°.

=> $\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^{o}$

=> x = $360^{\circ}-(65^{\circ}+75^{\circ}+85^{\circ})=135^{\circ}$