I. ĐỊNH LÍ 

HĐ1: SGK-tr105

Khẳng định: "Nếu một góc có hai cạnh là hai tia phân giác của hai góc kề bù thì góc đó là góc vuông".

Nhận xét: Khẳng định trên có các đặc điểm sau:

• Là một phát biểu về tính chất toán học.
• Tính chất toán học đó đã được chứng tỏ là đúng không dựa vào các trực giác hay đo đạc,..

=> Khẳng định có các đặc điểm như trên thường được gọi là định lí.

HĐ2: 

• Phần nằm giữa từ “ Nếu” và từ “ thì” là: một đường thẳng cắt hai đường thẳng song song
• Phần nằm sau từ “thì” là: hai góc so le trong bằng nhau.

Ví dụ 1: SGK -tr106

Luyện tập 1.

Giả thiết: một đường thẳng c cắt hai đường thẳng a, b và trong số các góc tạo thành có một cặp góc so le trong bằng nhau

Kết luận: hai đường thẳng a, b song song với nhau.

II. CHỨNG MINH ĐỊNH LÍ 

a) Vẽ hình:

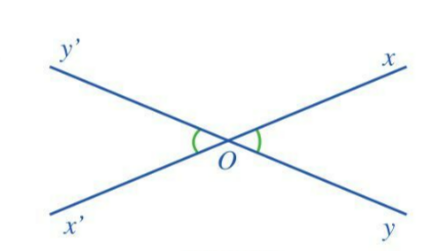
b) Viết giả thiết, kết luận

c) Chứng minh định lí:

Ta có: $\widehat{A_{1}}=\widehat{B_{1}}$ (giả thiết)

$\widehat{A_{3}}=\widehat{A_{1}}$ (hai góc đối đỉnh)

$=>\widehat{A_{3}}=\widehat{B_{1}}$ (cùng bằng $\widehat{A_{1}}$)

Mà $\widehat{A_{2}}+\widehat{A_{3}}=180^{0}$; $\widehat{B_{1}}+\widehat{B_{4}}=180^{0}$ (hai góc kề bù)

$=>\widehat{A_{2}}=\widehat{B_{4}}$

Ví dụ 2: SGK -tr107