CHƯƠNG IV: VECTƠ

BÀI 10. VECTƠ TRONG MẶT PHẲNG TỌA ĐỘ

1. TỌA ĐỘ CỦA VECTƠ

HĐ1: 

Do A biểu diễn số 1, M biểu diễn số 4, nên hai vectơ $\underset{OA}{\rightarrow}$ và $\underset{OM}{\rightarrow}$ có cùng phương, cùng hướng và |$\underset{OM}{\rightarrow}$|=4|$\underset{OA}{\rightarrow}$|.

Suy ra $\underset{OM}{\rightarrow}$=4$\underset{OA}{\rightarrow}$=4$\underset{i}{\rightarrow}$.

Cũng vậy, do A biểu diễn số 1, N biểu diễn số -$\frac{3}{2}$ nên hai vectơ $\underset{OA}{\rightarrow}$ và $\underset{ON}{\rightarrow}$ có cùng phương, ngược hướng và |$\underset{ON}{\rightarrow}$|=$\frac{3}{2}$|$\underset{OA}{\rightarrow}$|.

Suy ra $\underset{ON}{\rightarrow}$=-$\frac{3}{2} \underset{OA}{\rightarrow}$=-$\frac{3}{2} \underset{i}{\rightarrow}$.

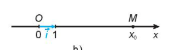
- Trục tọa độ (còn gọi là trục, hay trục số) là một đường thẳng mà trên đó đã xác định một điểm O và một vectơ $\underset{i}{\rightarrow}$ có độ dài bằng 1. 

Điểm O gọi là gốc tọa độ, vectơ $\underset{i}{\rightarrow}$ gọi là vectơ đơn vị của trục. Điểm M trên trục biểu diễn số xo nếu $\underset{OM}{\rightarrow}$=x$_{1} \underset{i}{\rightarrow}$.

HĐ2:

a) $\underset{OM}{\rightarrow}$=3$\underset{i}{\rightarrow}$+5$\underset{j}{\rightarrow}$,$\underset{ON}{\rightarrow}$=-2$\underset{i}{\rightarrow}$+$\frac{5}{2} \underset{j}{\rightarrow}$.

b) Vì $\underset{MN}{\rightarrow}$=$\underset{ON}{\rightarrow}$-$\underset{OM}{\rightarrow}$ nên

$\underset{MN}{\rightarrow}$=(-2$\underset{i}{\rightarrow}$+$\frac{5}{2} \underset{j}{\rightarrow}$)-(3$\underset{i}{\rightarrow}$+5$\underset{j}{\rightarrow}$)=-5$\underset{i}{\rightarrow}$-$\frac{5}{2} \underset{j}{\rightarrow}$.

Kết luận:

- Trên mặt phẳng với một đơn vị đo độ dài cho trước, xét hai trục Ox, Oy có chung gốc O và vuông góc với nhau. Kí hiệu vectơ đơn vị của trục Ox là $\underset{i}{\rightarrow}$, vectơ đơn vị của trục Oy là $\underset{j}{\rightarrow}$. Hệ gồm hai trục Ox, Oy như vậy được gọi là hệ trục tọa độ Oxy. Điểm O gọi là gốc tọa độ, trục Ox được gọi là hệ trục hoành, trục Oy gọi là trục tung.

Mặt phẳng chứa hệ trục tọa độ Oxy gọi là mặt phẳng tọa độ Oxy hay mặt phẳng Oxy.

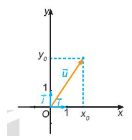
- Với mỗi vectơ $\underset{u}{\rightarrow}$ trên mặt phẳng Oxy, có duy nhất cặp số (x$_{0}$;y$_{0}$) sao cho $\underset{u}{\rightarrow}$=x$_{0} \underset{i}{\rightarrow}$+y$_{0} \underset{j}{\rightarrow}$. Ta nói vectơ $\underset{u}{\rightarrow}$ có tọa độ (x$_{0}$;y$_{0}$) và viết $\underset{u}{\rightarrow}$=(x$_{0}$;y$_{0}$) hay $\underset{u}{\rightarrow}$(x$_{0}$;y$_{0}$). Các số x$_{0}$,y$_{0}$ tương ứng được gọi là hoành độ, tung độ của $\underset{u}{\rightarrow}$.

Nhận xét: Hai vectơ bằng nhau khi và chỉ khi chúng có cùng tọa độ.

$\underset{u}{\rightarrow}$(x;y)=$\underset{v}{\rightarrow}$(x';y')⇔{x=x'  y=y'

Ví dụ 1 (SGK -tr61)

Luyện tập 1:

$\underset{0}{\rightarrow}$(0;0)

2. BIỂU THỨC TỌA ĐỘ CỦA CÁC PHÉP TOÁN VECTƠ 

HĐ3:

a) $\underset{u}{\rightarrow}$=2$\underset{i}{\rightarrow}$-3$\underset{j}{\rightarrow}$,$\underset{v}{\rightarrow}$=4$\underset{i}{\rightarrow}$+$\underset{j}{\rightarrow}$,$\underset{a}{\rightarrow}$=8$\underset{i}{\rightarrow}$-12$\underset{j}{\rightarrow}$.

b) Vì u$\underset{u}{\rightarrow}$+$\underset{v}{\rightarrow}$=(2$\underset{i}{\rightarrow}$-3$\underset{j}{\rightarrow}$)+(4$\underset{i}{\rightarrow}$+$\underset{j}{\rightarrow}$)=6$\underset{i}{\rightarrow}$-2$\underset{j}{\rightarrow}$

nên $\underset{u}{\rightarrow}$+$\underset{v}{\rightarrow}$=(6;-2).

Vì $\underset{u}{\rightarrow}$=2$\underset{i}{\rightarrow}$-3$\underset{j}{\rightarrow}$ nên 4$\underset{u}{\rightarrow}$=8$\underset{i}{\rightarrow}$-12$\underset{j}{\rightarrow}$.

Suy ra 4$\underset{u}{\rightarrow}$=(8;12).

c) Vì $\underset{a}{\rightarrow}$=8$\underset{i}{\rightarrow}$-12$\underset{j}{\rightarrow}$=4(2$\underset{i}{\rightarrow}$-3$\underset{j}{\rightarrow}$) và 

$\underset{u}{\rightarrow}$=2$\underset{i}{\rightarrow}$-3$\underset{j}{\rightarrow}$ nên $\underset{a}{\rightarrow}$=4$\underset{u}{\rightarrow}$.

Kết luận:

Cho hai vectơ $\underset{u}{\rightarrow}$=(x;y) và $\underset{v}{\rightarrow}$=(x';y'). Khi đó:

$\underset{u}{\rightarrow}$+$\underset{v}{\rightarrow}$=(x+x';y+y')

$\underset{u}{\rightarrow}$-$\underset{v}{\rightarrow}$=(x-x';y-y')

k$\underset{u}{\rightarrow}$=(kx;ky) với k∈R.

Ví dụ 2 (SGK -tr 62)

Nhận xét: Vectơ $\underset{v}{\rightarrow}$(x';y') cùng phương với vectơ $\underset{u}{\rightarrow}$(x;y)≠0 khi và chỉ khi tồn tại số k sao cho x' = kx, y' = ky (hay là $\frac{x'}{x}$=$\frac{y'}{y}$nếu xy≠0).

HĐ4: 

a) Trên trục Ox, điểm P biểu diễn số x$_{0}$:

$\underset{OP}{\rightarrow}$=x$_{0} \underset{i}{\rightarrow}$,|$\underset{OP}{\rightarrow}$|=|x$_{0}$|.|$\underset{i}{\rightarrow}$|=|x$_{0}$|.

b) Trên trục Oy, điểm Q biểu diễn số y$_{0}$:

$\underset{OQ}{\rightarrow}$=y$_{0} \underset{j}{\rightarrow}$,|$\underset{OQ}{\rightarrow}$|=|y$_{0}$|.|$\underset{j}{\rightarrow}$|=|y$_{0}$|.

c) Hình chữ nhật OPMQ có độ dài hai cạnh OP = |x$_{0}$| và OQ = |y$_{0}$|, suy ra độ dài đường chéo

OM=$\sqrt{OP^{2}+OQ^{2}}$=$\sqrt{x_{0}^{2}+y_{0}^{2}}$.

d) Áp dụng quy tắc hình bình hành, ta được $\underset{OM}{\rightarrow}$=$\underset{OP}{\rightarrow}$+$\underset{OQ}{\rightarrow}$=x$_{0} \underset{i}{\rightarrow}$+y$_{0} \underset{j}{\rightarrow}$.

Kết luận:

Nếu điểm M có tọa độ (x; y) thì vectơ $\underset{OM}{\rightarrow}$ có tọa độ (x; y) và độ dài |$\underset{OM}{\rightarrow}$|=$\sqrt{x^{2}+y^{2}}$.

Nhận xét:

Với vectơ $\underset{u}{\rightarrow}$(x;y) thì |$\underset{u}{\rightarrow}$|=$\sqrt{x^{2}+y^{2}}$

HĐ5:

a) Theo HĐ4:

$\underset{OM}{\rightarrow}$(x;y), $\underset{ON}{\rightarrow}$(x';y').

b) Ta có: 

$\underset{MN}{\rightarrow}$=$\underset{ON}{\rightarrow}$-$\underset{OM}{\rightarrow}$

=(x'$\underset{i}{\rightarrow}$+y'$\underset{j}{\rightarrow}$)-(x$\underset{i}{\rightarrow}$+y$\underset{j}{\rightarrow}$)

=(x'-x)$\underset{i}{\rightarrow}$+(y'-y)$\underset{j}{\rightarrow}$

Suy ra $\underset{MN}{\rightarrow}$=(x'-x;y'-y).

c) Theo nhận xét:

MN=|$\underset{MN}{\rightarrow}$|=$\sqrt{(x'-x)^{2}+(y'-y)^{2}}$.

Kết luận:

Với hai điểm M(x; y) và N(x'; y') thì 

$\underset{MN}{\rightarrow}$=(x'-x;y'-y) và khoảng cách giữa hai điể M, N là MN=|$\underset{MN}{\rightarrow}$|=($\sqrt{(x'-x)^{2}+(y'-y)^{2}}$.

Ví dụ 3 (SGK -tr63)

Luyện tập 2:

a) Hai vectơ $\underset{OA}{\rightarrow}$=(2;1) và $\underset{OB}{\rightarrow}$=(3;3) không cùng phương (vì $\frac{2}{3} \neq \frac{1}{3}$). Do đó các điểm A, B, O không cùng nằm trên một đường thẳng. Vậy chúng không thẳng hàng.

b) OABM là một hình bình hành khi và chỉ khi $\underset{OA}{\rightarrow}$=$\underset{MB}{\rightarrow}$

Ta có: $\underset{OA}{\rightarrow}$(2;1) và $\underset{MB}{\rightarrow}$(3-x;3-y)

$\underset{OA}{\rightarrow}$=$\underset{MB}{\rightarrow}$

<=> {3-x=2  3-y=1 <=> x=1;y=2.

Vậy điểm cần tìm là M(1; 2).

Ví dụ 4 (SGK -tr63)

Chú ý:

+ Trung điểm M của đoạn thẳng AB có tọa độ là ($\frac{x_{A}+x_{B}}{2}$;$\frac{y_{A}+y_{B}}{2}$).

+ Trọng tâm G của tam giác ABC có tọa độ là ($\frac{x_{A}+x_{B}+x_{C}}{3}$;$\frac{y_{A}+y_{B}+y_{C}}{3}$).

Vận dụng:

Trong 12 giờ, tâm bão chuyển động thẳng đều từ điểm A(13,8; 108,3) đến điểm B(14,1; 106,3). Suy ra $\underset{AB}{\rightarrow}$=(0,3;-2).

Gọi M(x; y) là điểm ứng với vị trí tâm bão tại thời điểm 9 giờ. Khi đó

$\underset{AM}{\rightarrow}$=(x-13,8;y-108,3) và $\underset{AM}{\rightarrow}$=$\frac{9}{12} \underset{AB}{\rightarrow}$ hay 4$\underset{AM}{\rightarrow}$=3$\underset{AB}{\rightarrow}$.

Từ đó ta có hệ phương trình

{4(x-13,8)=3.0,3 4(y-108,3)=3.(-2)

Giải hệ ta được x = 108,525 và y = 106,8.