CHƯƠNG VII. BẤT PHƯƠNG TRÌNH BẬC HAI MỘT ẨN

BÀI 3. PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI

1. PHƯƠNG TRÌNH DẠNG $\sqrt{ax^{2}+bx+c}$=$\sqrt{dx^{2}+ex+f}$

HĐKP1:

Thay x = 2 và x = -4 vào phương trình ta thấy nó thỏa mãn phương trình. Vậy x = 2 và x = -4 là nghiệm của phương trình 

Mặc dù kết quả đúng nhưng  lời giải trên thiếu bước thử nghiệm lại kết quả

Kết luận:

- Để giải phương trình $\sqrt{ax^{2}+bx+c}$=$\sqrt{dx^{2}+ex+f}$ ta làm như sau:

Bước 1: Bình phương hai vế của phương trình để được phương trình 

ax$^{2}$+bx+c = dx$^{2}$+ex+f.

Bước 2: Giải phương trình nhận được ở Bước 1.

Bước 3: Thử lại xem các giá trị x tìm được ở Bước 2 có thỏa mãn phương trình đã cho hay không và kết lụận nghiệm.

Ví dụ 1: SGK – tr15

Thực hành 1:

$\sqrt{31x^{2}-58x+1}$=$\sqrt{10x^{2}-11x-19}$

=> 31x$^{2}$-58x+1=10x$^{2}$-11x-19

21x$^{2}$-47x+20=0

x=$\frac{4}{7}$ hoặc x=$\frac{5}{3}$

Thay lần lượt x vào phương trình ta thấy cả 2 nghiệm đều thỏa mãn phương trình

2. PHƯƠNG TRÌNH DẠNG $\sqrt{ax^{2}+bx+c}$=dx+e

HĐKP2:

Thay lần lượt các giá trị của x vào phương trình ta thấy cả hai đều thỏa mãn.   

Mặc dù kết quả đúng nhưng  lời giải trên thiếu bước thử nghiệm lại kết quả.

Kết luận:

- Để giải phương trình $\sqrt{ax^{2}+bx+c}$=dx+e, ta làm như sau:

Bước 1: Bình phương hai vế của phương trình để được phương trình  ax$^{2}$+bx+c = (dx+e)$^{2}$.

Bước 2: Giải phương trình nhận được ở Bước 1.

Bước 3: Thử lại xem các giá trị x tìm được ở Bước 2 có thỏa mãn phương trình đã cho hay không và kết lụận nghiệm.

Ví dụ 2: SGK – tr15

Thực hành 2:

$\sqrt{3x^{2}+27x-41}$=2x+3 

⇒3x$^{2}$+27x-41=(2x+3)$^{2}$ 

⇒3x$^{2}$+27x-41=4x$^{2}$+12x+9 

x$^{2}$-15x+50=0 

<=> x=10 hoặc x=5  

Thay lần lượt các giá trị trên vào phương trình đã cho, ta thấy x = 5 và x = 10 đều thỏa mãn.

Vậy nghiệm của phương trình đã cho là x = 10 hoặc x = 5.

Vận dụng:

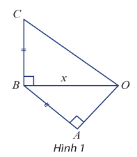
Xét tam giác vuông CBO có: ($\widehat{CBO}$=90$^{\circ}$)

CO$^{2}$=CB$^{2}$+BO$^{2}$=(x-1)$^{2}$+x$^{2}$=2x$^{2}$-2x+1 (ĐL Pytago)

⇒CO=$\sqrt{2x^{2}-2x+1}$ 

Xét tam giác vuông ABO có: ($\widehat{BAO}$=90$^{\circ}$)

BO$^{2}$=BA$^{2}$+AO$^{2}$ (ĐL Pytago)

⇒AO$^{2}$=BO$^{2}$-BA$^{2}$ 

=x$^{2}$-(x-1)$^{2}$ 

=2x-1 

⇒AO=$\sqrt{2x-1}$

a) OC = 3.OA

$\sqrt{2x^{2}-2x+1}$=3.$\sqrt{2x-1}$ (x > 1)

2x$^{2}$-2x+1=9.(2x-1) 

2x$^{2}$-20x+10=0 

=> x=5+2$\sqrt{5}$ (thỏa mãn điều kiện x > 1) hoặc x=5-2$\sqrt{5}$ (loại do x>1)

=> OB = 5+2$\sqrt{5}$-1 = 4+2$\sqrt{5}$  cm

b) OC=$\frac{5}{4}$OB

$\sqrt{2x^{2}-2x+1}$=$\frac{5}{4}$.x 

2x$^{2}$-2x+1=$\frac{25}{16}$.x${2}$ 

$\frac{7}{16}$x$^{2}$-2x+1=0 

x=4 (thỏa mãn x >1) hoặc x=$\frac{4}{7}$ (loại do x>1)

=> OB = 3 cm