Bài 1. Bổ sung vào chỗ chấm để được các phát biểu đúng:

a) Góc là hình được tạo bởi ........................

b) Góc xOy có đỉnh là ............................ và hai cạnh là ...............................

c) Góc ..................... có đỉnh là M và hai cạnh là MN và MP

Lời giải

 a) Góc là hình được tạo bởi hai tia chung gốc.

b) Góc xOy có đỉnh là O và hai cạnh là Ox và Oy.

c) Góc NMP có đỉnh là M và hai cạnh là MN và MP

Bài 2. Các góc nào có trong hình sau đây?

Hãy khoanh tròn vào những phương án phù hợp.

a) Góc ABC;               b) Góc ACD

c) Góc ADC;               d) Góc BCD

e) Góc EBD;               g) Góc AEB

Lời giải

Chọn phương án a), b), d)

Bài 3. Hãy kể tên các góc có trong mỗi hình vẽ dưới đây:

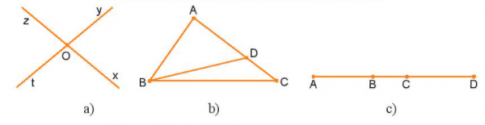
Lời giải

Hình a) có các góc: $\widehat{xOy};\widehat{yOz}; \widehat{zOt}; \widehat{tOx}; \widehat{xOz}; \widehat{yOt}$

Hình b) có các góc: $\widehat{BAC};\widehat{ABC}; \widehat{ABD}; \widehat{DBC}; \widehat{ADB}; \widehat{BDC};\widehat{ADC};\widehat{ACB}$

Hình c) gồm các góc: $\widehat{ABC};\widehat{ACD}$

Bài 4. Mỗi hình dưới đây có bao nhiêu góc?

Lời giải

- Hình a) có 6 góc

- Hình b) có 15 góc

Bài 5. Điểm M và N là điểm trong của những góc nào trong hình vẽ dưới đây?

Lời giải

M là điểm trong của góc x'At

N là điểm trong của góc x'Ay; x'At

Bài 6. Ba đường thẳng phân biệt có thể tạo ra bao nhiêu góc? Hãy vẽ hình trong các trường hợp đó.

Lời giải

Ba đường thẳng phân biệt có thể tạo ra số lượng góc khác nhau

Chẳng hạn:

- Ba đường thẳng tỏng hình a) tạo thành 15 góc

- Ba đường thẳng trong hình b) tạo thành 12 góc

- Ba đường thẳng trong hình c) tạo thành 18 góc

- Ba đường thẳng trong hình d) không tạo thành góc nào