A. PHƯƠNG PHÁP GIẢI

1. Ba điểm thẳng hàng

• Để nhận biết ba điểm có thẳng hàng không, ta kẻ đường thẳng đi qua hai điểm (trong số ba điểm đã cho) và xét xem điểm thứ ba (điểm còn lại) có thuộc đường thẳng vừa kẻ không (xem hình 6a và 6b), nếu nó thuộc đường thẳng vừa kẻ thì ba điểm đó là ba điểm thẳng hàng; ngược lại, chúng là ba điểm không thẳng hàng

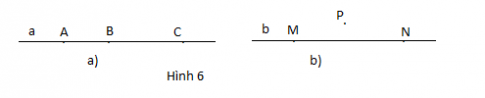
• Để nhận biết điểm B có nằm giữa hai điểm A và C không (một điểm nằm giữa hai điểm còn lại), ta vẽ đường thẳng AC và xét xem B có thuộc đường thẳng AC không; nếu có thì bằng trực giác để chỉ ra một điểm nằm giữa hai điểm còn lại.

Ví dụ 1: Trong hình bên hãy kể tên:

a) Các bộ ba điểm thẳng hàng.

b) Điểm nằm giữa hai điểm kia.

Hướng dẫn:

a) Các bộ ba điểm thẳng hàng là: (C, N, D) ; (M, N, P); (M, N, Q); (M, P, Q); (N, P, Q).

b) Điểm N nằm giữa hai điểm C và D; điểm N nằm giữa hai điểm M và P; điểm N nằm giữa hai điểm M và Q; điểm P nằm giữa hai điểm M và Q; điểm P nằm giữa hai điểm N và Q.

2. Đường thẳng đi qua hai điểm

Nếu hai đường thẳng a và b cắt nhau tại N thì ta có N $\in $ a và N $\in $ b. Ngược lại nếu M $\in $ c và M $\in $ d thì ta nói M là điểm chung của hai đường thẳng c và d.

Từ đó suy ra, muốn chứng tỏ hai đường thẳng trùng nhau, ta chỉ ra chúng có hai điểm chung.

Nếu có M $\in $ a, M $\in $ b và N $\in $ a, N  $\in $ b thì ta nói hai đường thẳng a và b trùng nhau

Ví dụ 2: Vẽ ba đường thẳng phân biệt sao cho số giao điểm của ba đường thẳng đó lần lượt là: 0, 1, 2 và 3.

Hướng dẫn:

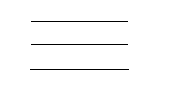
- Ba đường thẳng không có giao điểm (tức là chúng không cắt nhau). Đó là ba đường thẳng song song với nhau.

- Ba đường thẳng phân biệt có một giao điểm (tức là có một điểm chung). Vậy ba đường thẳng đó cắt nhau tại một điểm; đó là ba đường thẳng đồng quy.

- Ba đường thẳng phân biệt có hai giao điểm. Khi đó 1 đường thẳng cắt hai đường thẳng song song

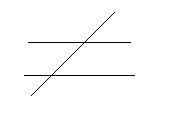
- Ba đường thẳng phân biệt có ba giao điểm. Khi đó ba đường thẳng đôi một cắt nhau.