1. NHẬN BIẾT (5 câu)

Câu 1: Trong các biểu thức sau, biểu thức nào là đa thức?

a) $x^{2}-3$          b) $x-1+\frac{1}{x}$          c) $\frac{3}{5}x+\frac{1}{2}xy^{2}$

d) $x^{2}yz-ab+b$           e) $\frac{x^{2}+2}{2022^{2}}$        f)$\frac{z}{x^{2}+1}+xz$

Giải:

Các biểu thức là đa thức là: 

a) $x^{2}-3$

c) $\frac{3}{5}x+\frac{1}{2}xy^{2}$

d) $x^{2}yz-ax+b$

e) $\frac{x^{2}+2}{2022^{2}}$

Câu 2: Biểu thức nào không là đa thức trong các biểu thức sau?

a) $xy^{2}-x^{3}z$  b)$2xy-\frac{5}{2x}$  c) $\frac{x^{2}+4y}{a^{2}-1}$ (a là hằng số)

d) $\frac{x^{2}+2y+z^{3}}{xy}$ e) $3x^{2}yz^{3}$  f)$3x^{2}+xy^{3}z-z$

g) $\frac{x^{2}+1}{a^{50}+1}$ (a là hằng số)

Giải:

Biểu thức không là đa thức là:

b) $2xy-\frac{5}{2x}$

d) $\frac{x^{2}+2y+z^{3}}{xy}$

Câu 3: Thu gọn đa thứ sau:

a) $A=2x^{2$}+x-\frac{1}{2}x^{2}+5x$

b) $B=y^{2}-2y+\frac{1}{2}y^{2}+5y-y^{2}$

c) $C=5xy+\frac{1}{2}x^{2}y-\frac{2}{3}xy+2x^{2}y$

 Giải:

a) $A=2x^{2$}+x-\frac{1}{2}x^{2}+5x$

$A=\left ( 2x^{2}-\frac{1}2{x^{2}} \right )+\left ( x+5x \right )$

$A=\frac{3}{2}x^{2}+6x$

b) $B=y^{2}-2y+\frac{1}{2}y^{2}+5y-y^{2}$

$B=(y^{2}+\frac{1}{2}y^{2}-y^{2})+(5y-2y)$

$B=\frac{1}{2}y^{2}+3y$

c)  $C=5xy+\frac{1}{2}x^{2}y-\frac{2}{3}xy+2x^{2}y$

 $C=(5xy-\frac{2}{3}xy)+(2x^{2}y+\frac{1}{2}x^{2}y)$

$C=\frac{13}{3}xy+\frac{5}{2}x^{2}y$

Câu 4: Thu gọn đa thức sau:

a) $M=\frac{1}{3}x^{2}y+xy^{2}-xy+\frac{1}{2}xy^{2}-5xy-\frac{1}{3}x^{2}y$

b) $N=5x^{2}y-3xy+\frac{1}{2}x^{2}y-xy+5xy-\frac{1}{3}x+\frac{1}{2}+\frac{2}{3}x-\frac{1}{4}$

Giải:

a) $M=\frac{1}{3}x^{2}y+xy^{2}-xy+\frac{1}{2}xy^{2}-5xy-\frac{1}{3}x^{2}y$

$M=(\frac{1}{3}x^{2}y-\frac{1}{3}x^{2}y)+(xy^{2}+\frac{1}{2}xy^{2})+(-5xy-xy)$

$M=\frac{3}{2}xy^{2}-6xy$

b) $N=5x^{2}y-3xy+\frac{1}{2}x^{2}y-xy+5xy-\frac{1}{3}x+\frac{1}{2}+\frac{2}{3}x-\frac{1}{4}$

$N=(5x^{2}y+\frac{1}{2}x^{2}y)+(-3xy-xy+5xy)+(-\frac{1}{3}x+\frac{2}{3}x)+(\frac{1}{2}-\frac{1}{4})$

$N=\frac{11}{2}x^{2}y+xy+\frac{1}{3}x+\frac{1}{4}$

Câu 5. Tìm bậc của các đa thức sau:

a) $x^{3}+2x-5xy+3x^{2}-x^{3}$

b) $y^{4}+4y^{2}-3y-3y^{4}$

c) $x^{2}+2x-xy+(-x)^{4}$

d) $y^{4}+y^{2}-y^{4}+x^{2}y^{2}$

Giải:

a) $x^{3}+2x-5xy+3x^{2}-x^{3}=3x^{2}-5xy+2x$

Vậy đa thức có bậc 2.

b) $y^{4}+4y^{2}-3y-3y^{4}=-2y^{4}+4y^{2}-3y$

Vậy đa thức có bậc 4

c) $x^{2}+2x-xy+(-x)^{4}=2x-xy$

Vậy đa thức có bậc 2

d) $y^{4}+y^{2}-y^{4}+x^{2}y^{2}=y^{2}+x^{2}y^{2}$

Vây đa thức có bậc 4

2. THÔNG HIỂU (5 câu)

Câu 1. Tìm bậc của đa thức sau:

c) $ax^{3}+2xy-5$ (a là hằng số) b) $ax^{2}+x^{2}-1$

Giải:

a) Nếu , đa thức có bậc 3

Nếu a = 0, đa thức có bậc 2

 b) Nếu , đa thức có bậc 2

Nếu a = 0, đa thức có bậc 2

Câu 2. Cho đa thức $A=6x^{2}y+50,5xy^{2}+x^{2}y-51,5xy^{2}$

a) Thu gọn A

b) Tìm bậc của A

c) Tính giá trị của A tại $x=\frac{-1}{7};y=14$

Giải:

a) Ta có:

$A=6x^{2}y+50,5xy^{2}+x^{2}y-51,5xy^{2}$

$A=(6x^{2}y+x^{2}y)+(50,5xy^{2}-51,5xy^{2})$

$A=7x^{2}y-xy^{2}$

b) Bậc của A bằng 3

c) Thay $x=\frac{-1}{7}$ ; y = 14 vào đa thức A, ta được:

 $A=7(\frac{-1}{7})^{2}.14-(\frac{-1}{7})14^{2}=2+28=30$

Câu 3: Cho đa thức $B=-2xy^{2}+\frac{1}{3}x^{3}y-x-\frac{1}{3}x^{3}y+xy^{2}+x-4x^{2}y$

a) Thu gọn B

b) Tìm bậc của B

c) Tính giá trị của B tại x = 1; y = 2

Giải:

a) Ta có: 

$B=-2xy^{2}+\frac{1}{3}x^{3}y-x-\frac{1}{3}x^{3}y+xy^{2}+x-4x^{2}y$

$B=(-2xy^{2}+xy^{2})+(\frac{1}{3}.x^{3}y-\frac{1}{3}x^{3}y)+(-x+x)-4x^{2}y$

$B=-xy^{2}-4x^{2}y$

b) Bậc của B bằng 3

c) Thay x =  1 và y = 2 vào đa thức B, ta được:

$B=-1.2^{2}-4.1^{1}.2=-4-8=-12$

Câu 4: Cho đa thức $M=ab+3a^{2}b+2a^{2}-2ab-3ab^{2}$

a) Thu gọn M

b) Tìm bậc của M và tính giá trị của M tại a = 2; b = 1.

Giải:

a) $M=ab+3a^{2}b+2a^{2}-2ab-3ab^{2}$

$M=(ab-2ab)+(3a^{2}b-3a^{2}b)+2a^{2}$

$M=-ab+2a^{2}$

b) Bậc của M bằng 2

Thay a = 2 và b = 1 vào M ta được:

 $M=-2.1+2.2^{2}=6$

Câu 5: Cho đa thức $P=2xy+\frac{1}{2}.x^{3}y^{2}-xy-\frac{1}{2}x^{3}y^{2}+y-1$

a) Thu gọn P

b) Tính giá trị của P tại x = 0,1; y = -2

Giải:

a) $P=2xy+\frac{1}{2}.x^{3}y^{2}-xy-\frac{1}{2}x^{3}y^{2}+y-1$

$P=(\frac{1}{2}.x^{3}y^{2}-\frac{1}{2}x^{3}y^{2})+(2xy-xy)+y-1$

$P=xy+y-1$

b) Thay x = 0,1 và y = -2 vào biểu thức P ta được:

 $P=0,1.(-2)-2-1=-3,2$

3. VẬN DỤNG (5 câu)

Câu 1: Cho a, b, c là những hằng số thoả mãn $a+b+c=2023$. Tính giá trị của các đa thức sau

a) $A=ax^{3}+bx^{2}y+cxy^{2}$ tại x = 1, y = 1

b) $B=ax^{2}y^{2}-bx^{4}y+cxy^{6}$ tại x = 1, y = -1

c) $B=axy+bx^{2}y^{2}-cx^{4}y$ tại x = -1, y = -1

Giải:

a) $A=ax^{3}+bx^{2}y+cxy^{2}$ tại x = 1, y = 1

Thay x = 1 và y = 1 vào A ta được:

$A=a.1^{3}+b.1^{2}.1+c.1.1^{2}=a+b+c+2023$

b) $B=ax^{2}y^{2}-bx^{4}y+cxy^{6}$ tại x = 1, y = -1

Thay x = 1 và y = -1 vào A ta được:

$B=ax^{2}y^{2}-bx^{4}y+cxy^{6}$

$=a.1^{2}.(-1)^{2}-b.1^{4}.(-1)+c.1.(-1)^{6}$

=a+b+c

=2023

c) $B=axy+bx^{2}y^{2}-cx^{4}y$ tại x = -1, y = -1

Thay x = -1 và y = -1 vào C ta được:

 $C=a.(-1).(-1)+b.(-1)^{2}.(-1)^{2}-c.(-1)^{4}.(-1)$

$C=a+b+c=2023$

Câu 2: 

a) Viết đa thức S biểu thị tổng diện tích các mặt của hình hộp chữ nhật có ba kích thước lần lượt là x (cm), 2y (cm), 3z (cm).

b) Tính giá trị của S tại x = 6; y = 2; z = 3

Giải: 

a) Giả sử gọi kích thước chiều rộng, chiều dài và độ cao của hình hộp chữ nhật lần lượt là x,2y,3z. Khi đó:

S = 2.3z(x + 2y) + 2x.2y = 6xz + 12yz + 4xy (cm2).

b) Tại x = 6; y = 2; z = 3 ta có:

S= 6.6.3 + 12.2.3 + 4.6.2 = 228 (cm2).

Câu 3: Viết biểu thức biểu thị thể tích V và diện tích xung quanh S của hình hộp chữ nhật trong hình. Tính giá trị của V, S khi x = 4 cm, y = 2 cm và z = 1 cm

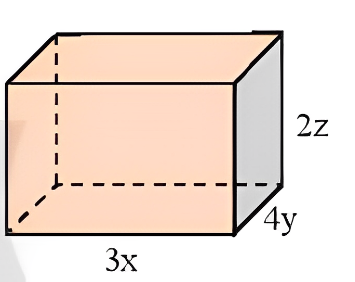
Giải:

V = 2x . 4y . 2z = 24.x.y.z ($cm^{3}$)

S=2 . 2z . (3x+4y) = 12.x.z + 16.y.z($cm^{2}$)

Thay x = 4, y = 2, z = 1 vào V ta có: 24 . 4 . 2 . 1 = 192 ($cm^{3}$)

Thay x = 4, y = 2, z = 1 vào S ta có: 12 . 4 . 1 + 16 . 2 . 1= 80 ($cm^{2}$)

Câu 4. Một bể bơi có dạng hình hộp chữ nhật với chiều dài là x (cm), chiều rộng là y(m). Ban đầu bể bơi đó không chứa nước. Buổi sáng, người ta bơm nước vào bể đến độ cao của mực nước là 1m. Buổi chiều, người ta tiếp tục bơm nước vào bể để độ cao của mực nước tăng thêm z(m). Viết đa thức biểu thị tổng thể tích nước trong bể sau hai lần bơm.

Giải:

Đa thức biểu thị tổng thể tích nước trong bể sau hai lần bơm là: 

V = x.y.1 + x.y z = x.y.(1+z)

Bài 5. Tìm đa thức biểu thị diện tích hình thang và tính diện tích hình thang đó biết x = 1; y = 1; z = 1

Giải:

Diện tích hình thang ABCD là:

S = $\frac{1}{2}$.(AB+DC).AH=$\frac{1}{2}$.(z+3y).2x = xz + 3xy (dvdt)

Tại x = 1; y =  1 và z = 1 ta có:

S = 1.1 + 3.1.1 = 4 (dvdt)

4. VẬN DỤNG CAO (4 câu)

Câu 1: Cho đa thức $f(x)=ax^{2}+bx+c$. Xác định các hệ số a, b, c biết: $f(0)=2;f(1)=7;f(-2)=-14$

Giải:

Theo bài ra ta có:

$f(0)=2 \Rightarrow 0+c =2 \Rightarrow c=2 (1)$

$f(1)=0 \Rightarrow a+b+c =7 \Rightarrow a+b=5 (2)$

$f(-2)=-14 \Rightarrow 4a+2b+2 =-14 \Rightarrow 2a-b=-8$

Từ (1) và (2) suy ra a = -1 và b = 6

Vậy đa thức cần tìm là: $f(x)=-x^{2}+6x+2$

Câu 2. Cho đa thức $A(x)=ax^{2}+bx+c$ biết A(0)=2021; A(1)=2022; A(-1)=2023. Tính f(-2).

Giải:

Theo gt ta có:

$A(0)=2021\Rightarrow c=2021$

$A(1)=2022\Rightarrow a+b+c=2022\Rightarrow a+b=1$

$A(-1)=2022\Rightarrow a-b+c=2023 \Rightarrow a-b=2$

$\Rightarrow a=\frac{3}{2};b=\frac{-1}{2}$

Khi đó đa thức có dạng: 

 $A(x)=\frac{3}{2}x^{2}-\frac{1}{2}x+2021\Rightarrow A(2)=2027$

Câu 3: Xác định đa thức bậc 3 biết: $B(0)=1;B(1)=0;B(2)=5;B(3)=22$

Giải:

Gọi đa thức cần tìm là: $B(x)=ax^{3}+bx^{2}+cx+d$

Theo bài ra ta có:

$B(0)=a.0^{3}+b.0^{2}+c.0+d \Rightarrow d=1$

$B(0)=a+b+2=7\Rightarrow d=1$

$B(1)=0\Rightarrow a+b+c=-1 (1)$

$B(2)=5\Rightarrow 4a+2b+c=2(2)$

$B(3)=22\Rightarrow 9a+3b+c=7 (3)$

Từ (1), (2), (3) ta có hệ:

$B(x)=x^{}\left\{\begin{matrix} a+b+c=-1 &  & \\ 4a+2b+c =2&  & \\ a+3b+c= 7&  &\end{matrix}\right.$

Giải ra ta được: a = 1; b = 0; c = -2

Vậy đa thức cần tìm là: $B(x)=x^{3}-2x+1$