Soạn giáo án điện tử Toán 8 KNTT Bài: Luyện tập chung (chương 9 tr.91)

Nội dung giáo án

CHÀO MỪNG CÁC EM

ĐẾN TIẾT HỌC HÔM NAY!

KHỞI ĐỘNG

Chia lớp thành 5 nhóm, thực hiện thực hiện làm bài toán sau

Cho  cân tại . Trên cạnh  lấy điểm , trên đoạn  lấy điểm  sao cho .

1. a) Chứng minh đồng dạng với
2. b) Chứng minh:

Giải

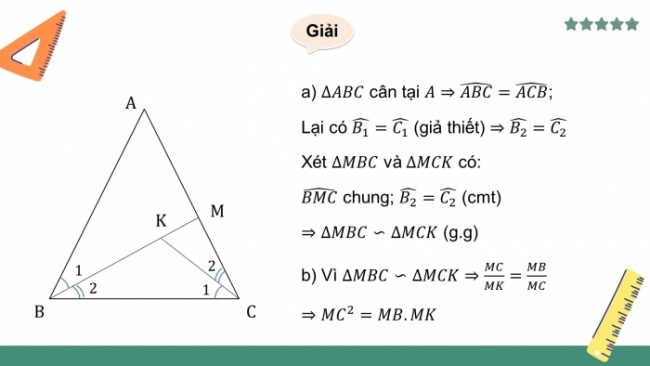
1. a) cân tại ;

Lại có  (giả thiết)  

Xét  và  có:

 chung;  (cmt)

  (g.g)

1. b) Vì  

CHƯƠNG IX. TAM GIÁC ĐỒNG DẠNG

LUYỆN TẬP CHUNG

(trang 91)

Nêu khái niệm và tính chất của hai tam giác đồng dạng?

• Khái niệm

Tam giác  gọi là đồng dạng với tam giác  nếu:

Tam giác  đồng dạng với tam giác  được kí hiệu      (viết theo thứ tự cặp đỉnh tương ứng).

Tỉ số  được gọi là     tỉ số đồng dạng của  với .

• Định lí

Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.

• Trường hợp đồng dạng thứ nhất

Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng với nhau.

• Trường hợp đồng dạng thứ hai

Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng với nhau.

• Trường hợp đồng dạng thứ ba

Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.

Ví dụ 1

Cho các điểm như Hình 9.26, biết rằng . Chứng minh rằng  và  

Hai tam giác  và  có:

Vậy  (c.c.c). Từ đó suy ra  

Do đó, // (có hai góc so le trong bằng nhau).

Vậy đường thẳng song song với cạnh  của tam giác  và cắt hai cạnh kéo dài lần lượt tại  và . Suy ra .

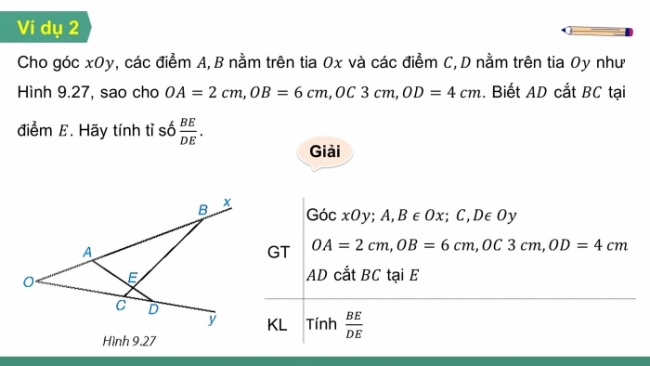
Cho góc , các điểm nằm trên tia  và các điểm nằm trên tia  như Hình 9.27, sao cho . Biết  cắt  tại điểm . Hãy tính tỉ số

Giải

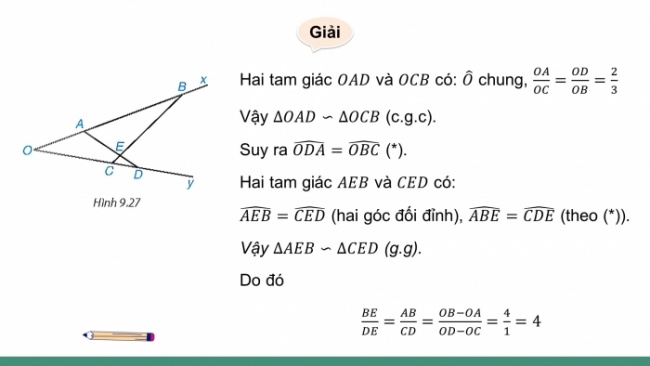
Hai tam giác  và  có:  chung,

Vậy  (c.g.c).

Suy ra  (*).

Hai tam giác  và  có:

 (hai góc đối đỉnh),  (theo (*)).

Vậy  (g.g).

Do đó

LUYỆN TẬP BẢO VỆ KHU PHỐ

--------------- Còn tiếp ---------------