Nội dung giáo án

CHÀO MỪNG CÁC EM ĐÃ ĐẾN VỚI TIẾT HỌC!

KHỞI ĐỘNG

Cho hai khối hộp chữ nhật: Khối hộp thứ nhất có ba kích thước là x, 2x và 3y; khối hộp thứ hai có diện tích đáy là 2xy. Tính chiều cao (cạnh) của khối hộp thứ hai, biết rằng hai khối hộp có cùng thể tích.

Thể tích của khối hộp thứ nhất: , bằng thể tích của khối hộp thứ hai. Để tính chiều cao của khối hộp thứ hai ta lấy  chia cho 2xy.

Vậy kết quả của phép chia này là bao nhiêu?

CHƯƠNG I. ĐA THỨC

BÀI 5. PHÉP CHIA ĐA THỨC CHO ĐƠN THỨC

NỘI DUNG BÀI HỌC

Chia đơn thức cho đơn thức

Chia đa thức cho đơn thức

1. CHIA ĐƠN THỨC CHO ĐƠN THỨC

HĐ 1:

Hãy nhớ lại cách chia đơn thức cho đơn thức trong trường hợp chúng có cùng một biến và hoàn thành các yêu cầu sau:

2. a) Thực hiện phép chia 6x³: 3x².
3. b) Với a, b ∈ ℝ và b ≠ 0; m, n ∈ ℕ, hãy cho biết:

• Khi nào thì ax^mchia hết cho bxⁿ.
• Nhắc lại cách thực hiện phép chia ax^mcho bxⁿ.

Trả lời:

a)

1. b) chia hết cho khi

Cách chia:

+ Lấy

+ Lấy

+ Nhân với

HĐ 2:

Với mỗi trường hợp sau, hãy đoán xem đơn thức A có chia hết cho đơn thức B không; nếu chia hết, hãy tìm thương của phép chia A cho B và giải thích cách làm:

1. a) b)

Trả lời:

1. a) A chia hết cho B

1. b) A không chia hết cho B

KẾT LUẬN

1. a) Đơn thức A chia hết cho đơn thức B (B ≠ 0) khi mỗi biến của B đều là biến của A với số mũ không lớn hơn số mũ của nó trong A.
2. b) Muốn chia đơn thức A cho đơn thức B (trường hợp chia hết), ta làm như sau:

• Chia hệ số của đơn thức A cho hệ số của đơn thức B;
• Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B;
• Nhân các kết quả tìm được với nhau.

Ví dụ 1:

Cho đơn thức

1. a) Giải thích tại sao không chia hết cho ?
2. b) Giải thích tại sao chia hết cho . Tìm thương của phép chia .

Giải

1. a) Ta thấy số mũ của trong bằng 2, lớn hơn số mũ của y trong  (bằng 1).

Do đó,  không chia hết cho .

1. b) chia hết cho vì tất cả các biến trong C có trong A và số mũ của các biến x và z trong C cùng bằng 2, không lớn hơn số mũ của x (bằng 2) và z (bằng 3) trong A.

Ta có:

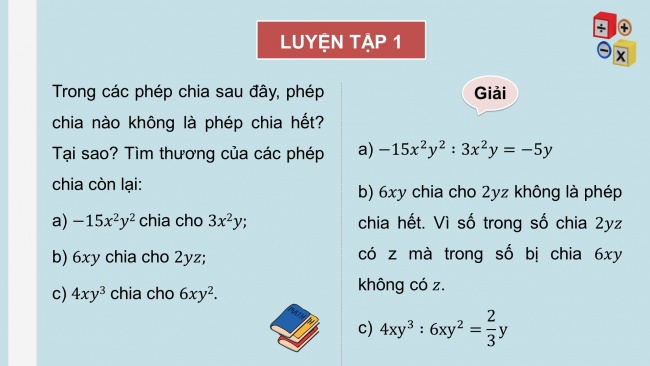
LUYỆN TẬP 1

Trong các phép chia sau đây, phép chia nào không là phép chia hết? Tại sao? Tìm thương của các phép chia còn lại:

1. a) chia cho
2. b) chia cho
3. c) chia cho

Giải

a)

1. b) chia cho không là phép chia hết. Vì số trong số chia  có z mà trong số bị chia  không có .

VẬN DỤNG 1

Giải bài toán mở đầu.

Cho hai khối hộp chữ nhật: Khối hộp thứ nhất có ba kích thước là x, 2x và 3y; khối hộp thứ hai có diện tích đáy là 2xy. Tính chiều cao (cạnh) của khối hộp thứ hai, biết rằng hai khối hộp có cùng thể tích.

Giải

Chiều cao của khối hộp thứ hai là:

2. CHIA ĐA THỨC CHO ĐƠN THỨC

KẾT LUẬN

• Đa thức A chia hết cho đơn thức B nếu mọi hạng tử của A đều chia hết cho B.
• Muốn chia đa thức A cho đơn thức B (trường hợp chia hết), ta chia từng hạng tử của A cho B rồi cộng các kết quả với nhau.

Ví dụ 2:

Thực hiện phép chia

Giải

LUYỆN TẬP 2

Làm tính chia

Giải

VẬN DỤNG 2

Tìm đa thức A sao cho

Giải

LUYỆN TẬP

--------------- Còn tiếp ---------------