Soạn giáo án điện tử Toán 8 CD Chương 5 Bài 1: Định lí Pythagore

THÂN MẾN CHÀO CÁC EM HỌC SINH ĐẾN VỚI BÀI HỌC MỚI

KHỞI ĐỘNG

Quan sát Hình 1, bạn Đan khẳng định rằng: Diện tích của hình vuông lớn nhất bằng tổng diện tích của hai hình vuông còn lại.

Bạn Đan dựa vào kiến thức nào để đưa ra khẳng định trên?

CHƯƠNG V: ĐỊNH LÍ PYTHAGORE. TỨ GIÁC

BÀI 1:

ĐỊNH LÍ PYTHAGORE

NỘI DUNG BÀI HỌC

Định lí Pythagore

Định lí Pythagore đảo

1. ĐỊNH LÍ PYTHAGORE

  Thảo luận nhóm đôi, hoàn thành HĐ1.

HĐ 1.

Thực hiện các hoạt động sau:

1. a) Vẽ và cắt giấy để có 4 hình tam giác vuông như nhau với độ dài cạnh huyền là a, độ dài hai cạnh góc vuông là b và c, trong đó a, b, c có cùng đơn vị độ dài (Hình 2).
2. b) Vẽ hình vuông ABCD có cạnh là b + c như Hình 3. Đặt 4 hình tam giác vuông đã cắt ở câu a lên hình vuông ABCD vừa vẽ, phần chưa bị che đi là hình vuông MNPQ với độ dài cạnh là a (Hình 4).
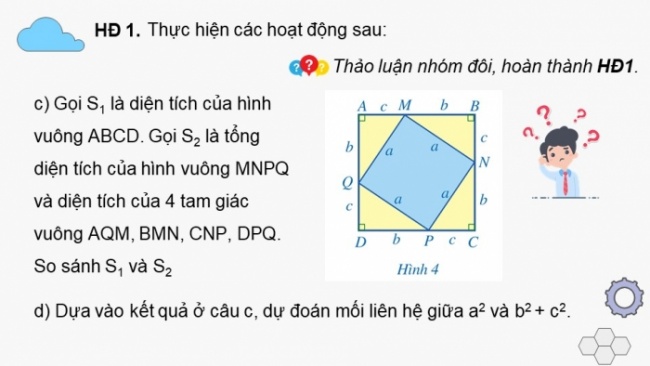
3. c) Gọi S₁là diện tích của hình vuông ABCD. Gọi S₂là tổng diện tích của hình vuông MNPQ và diện tích của 4 tam giác vuông AQM, BMN, CNP, DPQ. So sánh S₁ và S₂
4. d) Dựa vào kết quả ở câu c, dự đoán mối liên hệ giữa a²và b² + c².

Giải

1. c) là: (đơn vị diện tích).

 là:  (đơn vị diện tích).

 là:  (đơn vị diện tích).

Tổng diện tích của 4 tam giác vuông  là:

 (đơn vị diện tích).

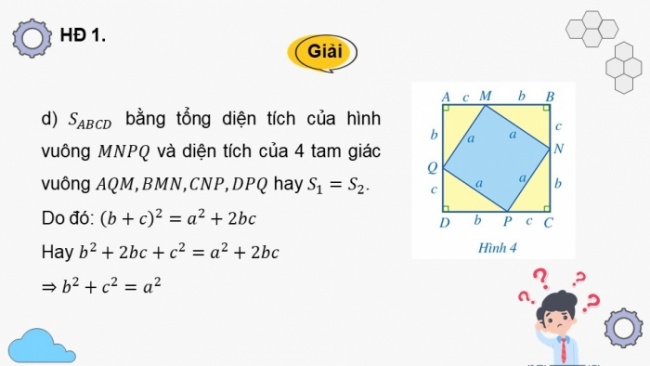
1. d) bằng tổng diện tích của hình vuông và diện tích của 4 tam giác vuông  hay .

Do đó:

Hay

KẾT LUẬN

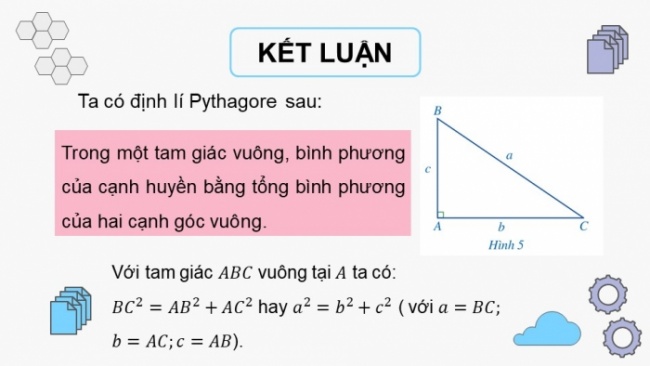
Ta có định lí Pythagore sau:

Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương của hai cạnh góc vuông.

Với tam giác  vuông tại  ta có:

 hay  ( với

).

Ví dụ 1: SGK – tr.95

                                   Cho tam giác ABC vuông tại A có AB = 5 cm và AC = 12 cm. Tính độ dài cạnh BC.

Giải

Do tam giác ABC vuông tại A nên theo định lí Pythagore, ta có:

Suy ra

Do đó  (cm)

Luyện tập 1

                        Tính độ dài đường chéo của hình vuông có độ dài cạnh là

Giải

Ta có hình vuông  độ dài các cạnh là . Đường chéo

          Áp dụng định lí Pythagore cho  vuông tại , có:

1. ĐỊNH LÍ PYTHAGORE ĐẢO

HĐ 2.

Thực hiện các hoạt động sau

1. a) Vẽ một tam giác ABC có AB = 3 cm, AC = 4 cm và BC = 5 cm;
2. b) Tính và so sánh diện tích của hình vuông có cạnh BC với tổng diện tích của hai hình vuông tương ứng có cạnh AB và AC (Hình 6);
3. c) Kiểm tra xem góc A của tam giác ABC có phải là góc vuông hay không.

Giải

a)

1. b) Diện tích của hình vuông có cạnh là:

Diện tích của hình vuông có cạnh  là:

Tổng diện tích của hai hình vuông trên là:

Diện tích của hình vuông có cạnh  là:

Vậy diện tích của hình vuông có cạnh  bằng tổng diện tích của hai hình vuông tương ứng có cạnh  và .

1. c) Dùng thước êke (hoặc thước đo góc) ta xác định được của là góc vuông.

KẾT LUẬN

Ta có định lí Pythagore đảo sau:

Nếu một tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh còn lại thì tam giác đó là tam giác vuông.

Với tam giác , nếu

 hay  ( với

) thì tam giác ABC vuông tại A

Ví dụ 2: SGK – tr.96

Cho tam giác DEG có DE = 7 cm, DG = 24 cm và EG = 25 cm. Tam giác DEG có phải là tam giác vuông hay không?

Giải

Xét tam giác DEG, ta có:  ()

Và  ()

Suy ra

    Do đó tam giác DEG vuông tại D (theo định lí Pythagore đảo)

Thực hành 2

                       Tam giác có ba cạnh 20 cm, 21 cm, 29 cm có phải là tam giác vuông hay không?

Giải

Ta có:  ()

Và  ()

Suy ra

 Tam giác có ba cạnh 20 cm, 21 cm, 29 cm là tam giác vuông (theo định lí Pythagore đảo)

Ví dụ 3: SGK – tr.96

                                   Hình 8 mô tả một cánh buồm có dạng tam giác vuông, được buộc vào cột buồm thẳng đứng, với độ dài hai cạnh góc vuông là 12 m và 5 m. Tính chu vi và diện tích của cánh buồm đó

Giải

Gọi  (m) là độ dài cạnh huyền của cánh buồm ()

Theo định lí Pythagore, ta có:

Suy ra  (m)

Chu vi của cánh buồm đó là: 12 + 5 + 13 = 30 (m)

Diện tích của cánh buồm đó là:  ()

LUYỆN TẬP 

--------------- Còn tiếp ---------------