Soạn giáo án điện tử Toán 8 CD Chương 3 Bài 2: Mặt phẳng tọa độ. Đồ thị của hàm số

NHIỆT LIỆT CHÀO MỪNG CÁC EM
ĐẾN VỚI BÀI HỌC HÔM NAY

KHỞI ĐỘNG

Ở lớp 6, ta đã biết rằng mỗi điểm trên bản đồ địa lí được xác định bởi một cặp số (tọa độ địa lí) là kinh độ và vĩ độ. Chẳng hạn, tọa độ địa lí của hồ Hoàn Kiếm ở Thủ đô Hà Nội là: .

Trong toán học, cặp số để xác định vị trí của một điểm trên mặt phẳng được gọi là gì?

BÀI 2: MẶT PHẲNG TỌA ĐỘ. ĐỒ THỊ CỦA HÀM SỐ

NỘI DUNG BÀI HỌC

Mặt phẳng tọa độ

Tọa độ của một điểm trong mặt phẳng tọa độ

Đồ thị của hàm số

PHẦN I

MẶT PHẲNG TỌA ĐỘ

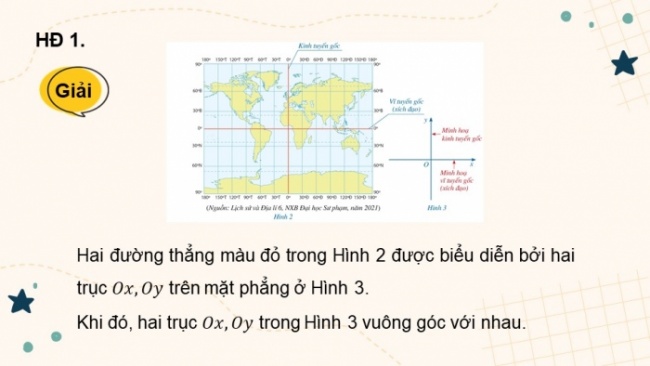
HĐ 1.

Hình 2 là một dạng phép chiếu bản đồ có các đường kinh tuyến và vĩ tuyến đều là các đường thẳng, trong đó kinh tuyến gốc và vĩ tuyến gốc được minh họa bằng hai đường thẳng màu đỏ.

Chúng được biểu diễn bởi hai trục Ox, Oy trên mặt phẳng ở Hình 3. Nêu nhận xét về hai trục Ox, Oy.

Giải

Hai đường thẳng màu đỏ trong Hình 2 được biểu diễn bởi hai trục  trên mặt phẳng ở Hình 3.

Khi đó, hai trục  trong Hình 3 vuông góc với nhau.

ĐỊNH NGHĨA

Trên mặt phẳng, ta vẽ hai trục số  vuông góc với nhau và cắt nhau tại gốc  của mỗi trục. Khi đó ta có hệ trục tọa độ .

Trục  gọi là trục tọa độ.  gọi là trục hoành,  gọi là trục tung.  gọi là gốc tọa độ.

Mặt phẳng có hệ trục tọa độ  gọi là mặt phẳng tọa độ .

Lưu ý

Hai trục tọa độ chia mặt phẳng thành bốn góc: góc phần tư thứ I, góc phần tư thứ II, góc phần tư thứ III, góc phần tư thứ IV theo thứ tự ngược chiều kim đồng hồ.

Các đơn vị độ dài trên hai trục tọa độ được chọn bằng nhau (nếu không có lưu ý gì thêm).

Ví dụ 1

Màn hình ra đa của đài kiểm soát không lưu gợi nên hình ảnh một mặt phẳng tọa độ (Hình 5). Ba chấm sáng trên màn hình ra đa nằm ở góc phần tư nào của mặt phẳng tọa độ

Giải

Cả ba chấm sáng trên màn hình ra đa của đài kiểm soát không lưu đều nằm ở góc phần tư thứ II của mặt phẳng tọa độ.

PHẦN II

TỌA ĐỘ CỦA MỘT ĐIỂM
TRONG MẶT PHẲNG TỌA ĐỘ

Cho điểm M trong mặt phẳng tọa độ Oxy (Hình 6).

1. a) Hình chiếu của điểm M trên trục hoành Ox là điểm nào trên trục số Ox?
2. b) Hình chiếu của điểm M trên trục tung Oy là điểm nào trên trục số Oy?

HĐ 2.

1. a) Hình chiếu của điểm trên trục hoành là điểm  trên trục .
2. b) Hình chiếu của điểm trên trục hoành là điểm  trên trục .

Chú ý: Cặp Cặp số  gọi là tọa độ điểm  trong mặt phẳng tọa độ.

ĐỊNH NGHĨA

Cho điểm  trong mặt phẳng tọa độ

Giả sử hình chiếu của điểm  lên trục hoành  là điểm  trên trục số , hình chiếu của điểm  lên trục tung  là điểm  trên trục .

Cặp số  gọi là tọa độ của điểm ,  là hoành độ và  là tung độ của điểm

Điểm  có tọa độ  được kí hiệu .

Trong mặt phẳng tọa độ , mỗi điểm  xác định một cặp số . Ngược lại, mỗi cặp số  xác định một điểm .

Ví dụ 2

Cho mặt phẳng tọa độ  như hình 8. Xác định tọa độ các điểm

Giải

Tọa độ các điểm  lần lượt là:  

Nhận xét + Điểm nằm trên trục hoành có tung độ bằng 0.

                   + Điểm nằm trên trục tung có hoành độ bằng 0.

--------------- Còn tiếp ---------------