Soạn giáo án điện tử toán 11 CTST Chương 8 Bài 2: Đường thẳng vuông góc với mặt phẳng

Nội dung giáo án

CHÀO MỪNG CÁC EM ĐẾN VỚI BÀI GIẢNG HÔM NAY

KHỞI ĐỘNG

Trong thực tế, người thợ xây dựng thường dùng dây dọi để xác định đường vuông góc với nền nhà. Thế nào là đường thẳng vuông góc với mặt phẳng?

BÀI 2: ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG

NỘI DUNG BÀI HỌC

Đường thẳng vuông góc với mặt phẳng

Liên hệ giữa tính song song và tính vuông góc của đường thẳng và mặt phẳng

Phép chiếu vuông góc

1. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG

                                      Thả một dây dọi  chạm sàn nhà tại điểm . Kẻ một đường thẳng  bất kì trên sàn nhà.

1. a) Dùng êke để kiểm tra xem có vuông góc vớikhông.
2. b) Nêu nhận xét về góc giữa dây dọi và một đường thẳng bất kì trong sàn nhà.

Giải

1. a) vuông góc với ,
2. b) Dây dọi vuông góc với mọi đường thẳng trong mặt phẳng sàn nhà.

ĐỊNH NGHĨA

Đường thẳng  gọi là vuông góc với mặt phẳng  nếu nó vuông góc với mọi đường thẳng  nằm trong , kí hiệu .

Ví dụ 1: SGK – tr.57

                                                             Cho biết cột trụ gôn của một sân bóng đá là đường thẳng vuông góc với mặt sân (Hình 3). Tìm góc giữa  và một đường thẳng  kẻ trên sân.

Giải

Do đường thẳng  vuông góc với mặt sân suy ra  vuông góc với mọi đường thẳng nằm trên mặt sân. Vậy ta có góc giữa  và  bằng .

HĐKP2:

                                Cho đường thẳng  vuông góc với hai đường thẳng 2 cắt nhau  và  trong mặt phẳng . Xét một đường thẳng  bất kì trong  

( không song song với  và ).

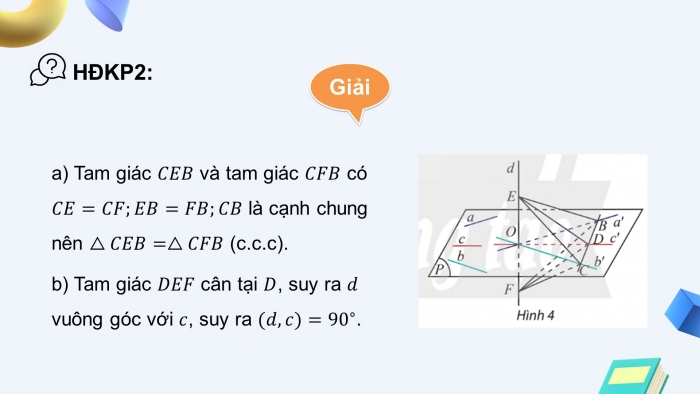
Gọi  là giao điểm của  và . Trong  vẽ qua  ba đường thẳng lần lượt song song với . Vẽ một đường thẳng cắt  lần lượt tại . Trên  lấy hai điểm  sao cho là trung điểm của  (Hình 4).

1. a) Giải thích tại sao hai tam giác và bằng nhau
2. b) Có nhận xét gì về tam giác ? Từ đó suy ra góc giữa và

Giải

1. a) Tam giác và tam giác có  là cạnh chung nên  (c.c.c).
2. b) Tam giác cân tại , suy ra vuông góc với , suy ra .

KẾT LUẬN

ĐỊNH LÍ 1

Nếu đường thẳng  vuông góc với hai đường thẳng cắt nhau  và  cùng nằm trong mặt phẳng  thì .

Ví dụ 2: SGK – tr.58

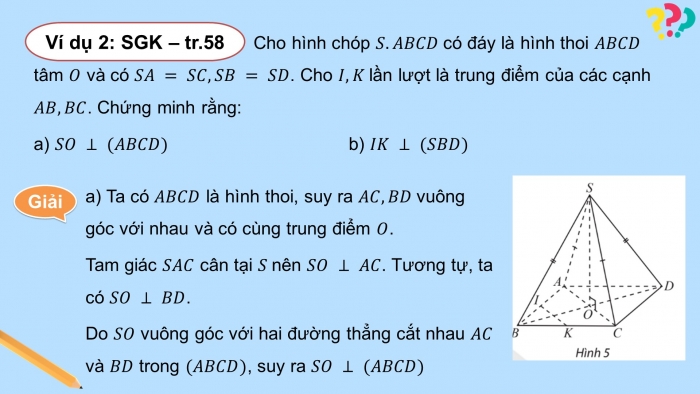
                                                            Cho hình chóp có đáy là hình thoi  tâm  và có . Cho lần lượt là trung điểm của các cạnh . Chứng minh rằng:

1. a) b)

Giải

1. a) Ta có là hình thoi, suy ra vuông góc với nhau và có cùng trung điểm .

Tam giác  cân tại nên . Tương tự, ta có .

Do  vuông góc với hai đường thẳng cắt nhau  và  trong , suy ra

1. b) Ta có và , do đó

Ta có , do đó

Từ và suy ra

Thảo luận nhóm đôi, hoàn thành HĐKP3.

1. a) Trong không gian, cho điểm  và đường thẳng . Gọi  là hai đường thẳng phân biệt đi qua  và vuông góc với  (Hình 6a). Có nhận xét gì về vị trí tương đối giữa đường thẳng  và ?
2. b) Trong không gian, cho điểm  và mặt phẳng . Gọi  và  là hai mặt phẳng đi qua  và lần lượt vuông góc với hai đường cắt nhau  nằm trong  (Hình 6b). Có nhận xét gì về vị trí giữa mặt phẳng  và giao tuyến  của ?

Giải

1. a) vuông góc với
2. b) Ta có:

  vuông góc với

KẾT LUẬN

ĐỊNH LÍ 2

Có duy nhất một mặt phẳng đi qua một điểm và vuông góc với một đường thẳng cho trước.

Có duy nhất một đường thẳng đi qua một điểm và vuông góc với một mặt phẳng cho trước.

Ví dụ 3: SGK – tr.58

1. a) Cho hình chóp có các cạnh bên bằng nhau, đáy là hình vuông tâm (Hinh 7a). Gọi d là đường thẳng đi qua và vuông góc với mặt phẳng (). Chứng minh  đi qua  
2. b) Cho đoạnn thằng có à trung điểm. Gọi là mặt phẳng di qua  và vuông góc vói là hai điểm cách đều hai đầu của đoạn thẳng  sao cho không thẳng hàng (Hình 7b). Chứng minh  và  thuộc mặt phẳng .
3. a) Ta có: suy ra , suy ra .

Suy ra .

Theo giả thiết, ta có đường thẳng  đi qua  và vuông góc với . Do qua điểm  chi có duy nhất một đường thẳng vuông góc với nên  phải trùng với đường thẳng , suy ra  đi qua .

1. b) Ta có: suy ra , suy ra .

Suy ra .

Theo giả thiết, ta có  là mặt phằng đi qua  và vuông góc với . Do qua điểm  chi có duy nhất một mặt phằng vuông góc với  nên  phải trùng với suy ra  và  thuộc .

Thực hành 1