Bài giảng điện tử dạy thêm Toán 12 KNTT Bài tập cuối chương I

Nội dung giáo án

CHÀO MỪNG CẢ LỚP ĐẾN VỚI TIẾT HỌC HÔM NAY!

KHỞI ĐỘNG

Khảo sát và vẽ đồ thị của các hàm số sau:

Giải:

Tập xác định:

Hàm số đồng biến trên các khoảng và , nghịch biến trên khoảng

,

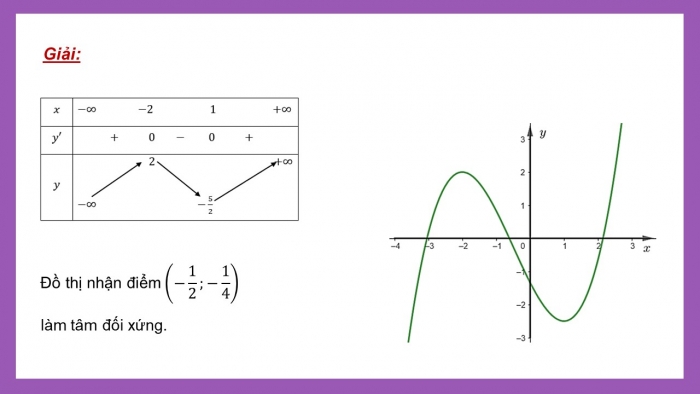
Bảng biến thiên:

làm tâm đối xứng.

Tập xác định:

Hàm số đồng biến trên các khoảng và . Hàm số không có cực trị.

đường thẳng là tiệm cận ngang của đồ thị hàm số.

đường thẳng là tiệm cận đứng của đồ thị hàm số.

Bảng biến thiên:

Tập xác định:

Hàm số đồng biến trên các khoảng và . Hàm số không có cực trị.

đường thẳng là tiệm cận ngang của đồ thị hàm số.

đường thẳng là tiệm cận đứng của đồ thị hàm số.

Bảng biến thiên:

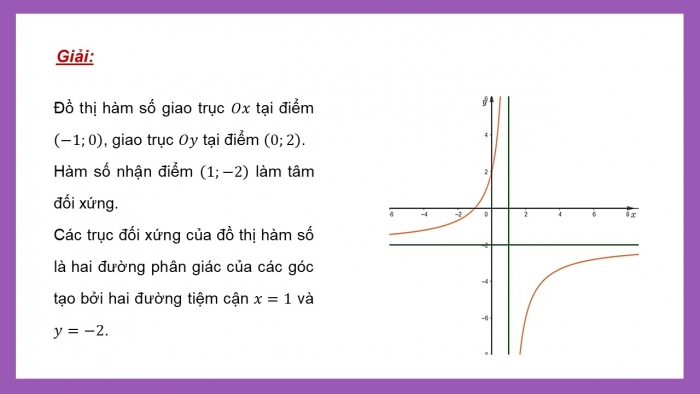
Đồ thị hàm số giao trục tại điểm , giao trục tại điểm .

Hàm số nhận điểm làm tâm đối xứng.

Các trục đối xứng của đồ thị hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận và .

Tập xác định:

Hàm số đồng biến trên các khoảng và . Hàm số không có cực trị.

Đường thẳng là tiệm cận xiên của đồ thị hàm số.

,

Đường thẳng là tiệm cận đứng của đồ thị hàm số.

,

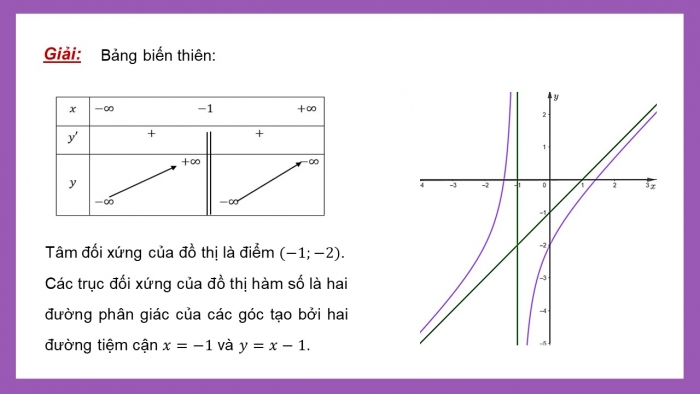
Bảng biến thiên:

Tâm đối xứng của đồ thị là điểm .

Các trục đối xứng của đồ thị hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận và .

CHƯƠNG 1: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ

BÀI TẬP CUỐI CHƯƠNG 1

PHIẾU BÀI TẬP SỐ 1

Bài 1. Cho hàm số là tham số.

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi .

b) Tìm để đồ thị hàm số có các điểm cực đại và cực tiểu nằm về hai phía của trục tung.

Giải:

a) Khi phương trình trở thành

Tập xác định:

Ta có:

Hàm số đồng biến trên khoảng ; hàm số nghịch biến trên khoảng và  

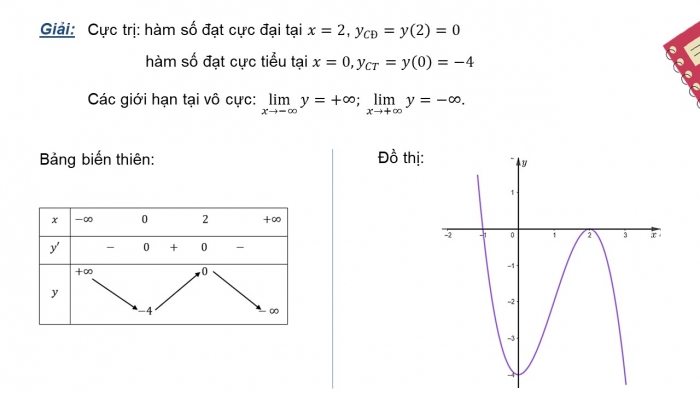
Cực trị: hàm số đạt cực đại tại ,

             hàm số đạt cực tiểu tại

Các giới hạn tại vô cực:

Bảng biến thiên:

Đồ thị:

b) Ta có:

Để hàm số có các điểm cực đại và cực tiểu nằm về hai phía của trục tung khi:

có hai nghiệm trái dấu

Vậy .

a) Khảo sát và vẽ đồ thị của hàm số.

b) Tìm trên đồ thị điểm sao cho tổng khoảng cách từ đến hai đường tiệm cận của là nhỏ nhất.

Giải:

Hàm số đồng biến trên các khoảng và . Hàm số không có cực trị.

đường thẳng là tiệm cận ngang của đồ thị hàm số.

đường thẳng là tiệm cận đứng của đồ thị hàm số.

Bảng biến thiên:

Hàm số nhận điểm làm tâm đối xứng.

Các trục đối xứng của đồ thị hàm số là hai đường phân giác của các góc tạo bởi hai đường tiệm cận và .

Khoảng cách từ đến tiệm cận đứng là:

Vậy tổng khoảng cách từ đến hai tiệm cận nhỏ nhất bằng 2 khi hoặc .

Bài 3. Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:

Giải:

--------------- Còn tiếp ---------------