Bài giảng điện tử dạy thêm Toán 12 KNTT Bài 10: Phương sai và độ lệch chuẩn
Tải giáo án điện tử dạy thêm Toán 12 Bài 10: Phương sai và độ lệch chuẩn chương trình mới sách kết nối tri thức. Giáo án điện tử này dùng để giảng dạy online hoặc trình chiếu buổi chiều hoặc buổi 2. Giáo án có nhiều hình ảnh đẹp, tư liệu sinh động. Chắc chắn bộ bài giảng này sẽ hỗ trợ tốt việc giảng dạy và đem đến sự hài lòng. Powerpoint dạy thêm Toán 12 KNTT








Còn nữa....Giáo án khi tải về là bản đầy đủ. Có full siles bài giảng!
Nội dung giáo án
THÂN MẾN CHÀO CÁC EM HỌC SINH ĐẾN VỚI BÀI HỌC MỚI
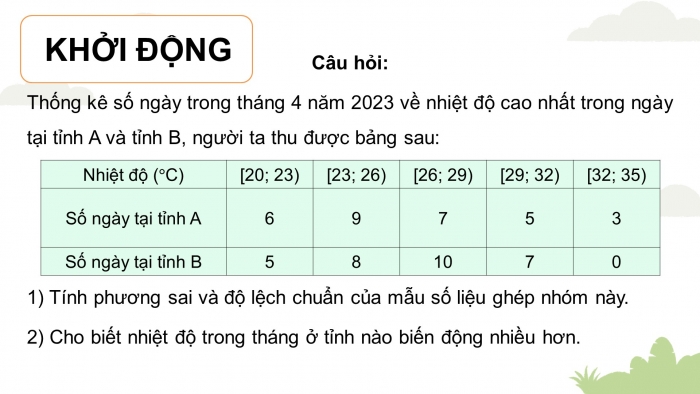
KHỞI ĐỘNG
Câu hỏi:
Thống kê số ngày trong tháng 4 năm 2023 về nhiệt độ cao nhất trong ngày tại tỉnh A và tỉnh B, người ta thu được bảng sau:
| Nhiệt độ ( | [20; 23) | [23; 26) | [26; 29) | [29; 32) | [32; 35) |
| Số ngày tại tỉnh A | 6 | 9 | 7 | 5 | 3 |
| Số ngày tại tỉnh B | 5 | 8 | 10 | 7 | 0 |
1) Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm này.
2) Cho biết nhiệt độ trong tháng ở tỉnh nào biến động nhiều hơn.
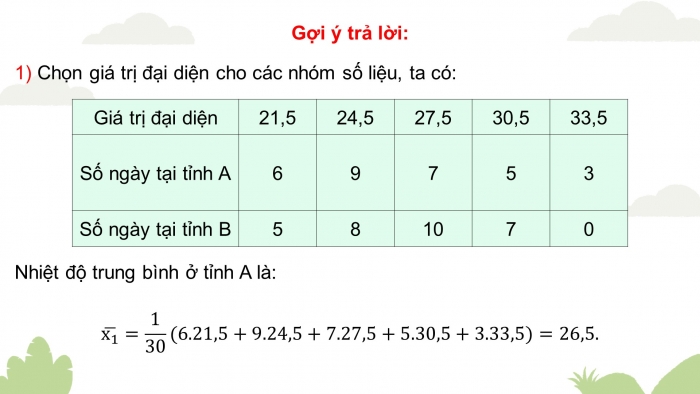
Gợi ý trả lời:
1) Chọn giá trị đại diện cho các nhóm số liệu, ta có:
| Giá trị đại diện | 21,5 | 24,5 | 27,5 | 30,5 | 33,5 |
| Số ngày tại tỉnh A | 6 | 9 | 7 | 5 | 3 |
| Số ngày tại tỉnh B | 5 | 8 | 10 | 7 | 0 |
Nhiệt độ trung bình ở tỉnh A là:
![]()
1) Nhiệt độ trung bình ở tỉnh B là:
![]()
Phương sai và độ lệch chuẩn của mẫu số liệu về nhiệt độ ở tỉnh A:

Phương sai và độ lệch chuẩn của mẫu số liệu về nhiệt độ ở tỉnh A:
![]()
2)
Vì ![]() nên nhiệt độ trong ngày của tỉnh A biến động nhiều hơn nhiệt độ trong ngày của tỉnh B.
nên nhiệt độ trong ngày của tỉnh A biến động nhiều hơn nhiệt độ trong ngày của tỉnh B.
BÀI 10:
PHƯƠNG SAI VÀ ĐỘ LỆCH CHUẨN
HỆ THỐNG KIẾN THỨC
1. Phương sai và độ lệch chuẩn
Phương sai của mẫu số liệu ghép nhóm, kí hiệu là ![]() , là một số được tính theo công thức sau:
, là một số được tính theo công thức sau: ![]()
trong đó, ![]() với
với ![]() là giá trị đại diện cho nhóm
là giá trị đại diện cho nhóm ![]() và
và ![]() là số trung bình của mẫu số liệu ghép nhóm.
là số trung bình của mẫu số liệu ghép nhóm.
Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu là ![]() , là căn bậc hai số học của phương sai của mẫu số liệu ghép nhóm, tức là
, là căn bậc hai số học của phương sai của mẫu số liệu ghép nhóm, tức là ![]() .
.
Nhận xét.
Ta có thể tính phương sai theo công thức:
![]()
Độ lệch chuẩn có cùng đơn vị với đơn vị của mẫu số liệu.
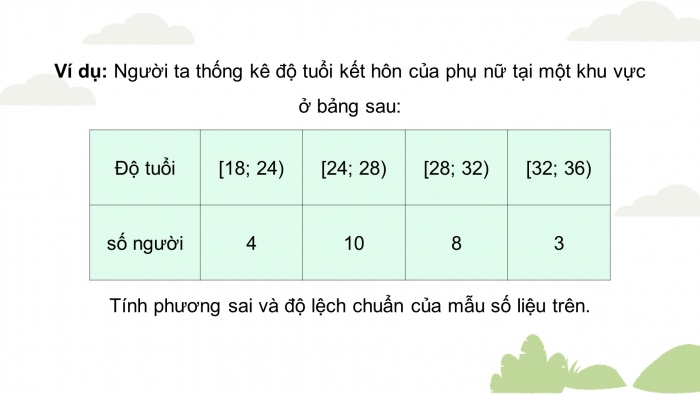
Ví dụ: Người ta thống kê độ tuổi kết hôn của phụ nữ tại một khu vực ở bảng sau:
| Độ tuổi | [18; 24) | [24; 28) | [28; 32) | [32; 36) |
| số người | 4 | 10 | 8 | 3 |
Tính phương sai và độ lệch chuẩn của mẫu số liệu trên.
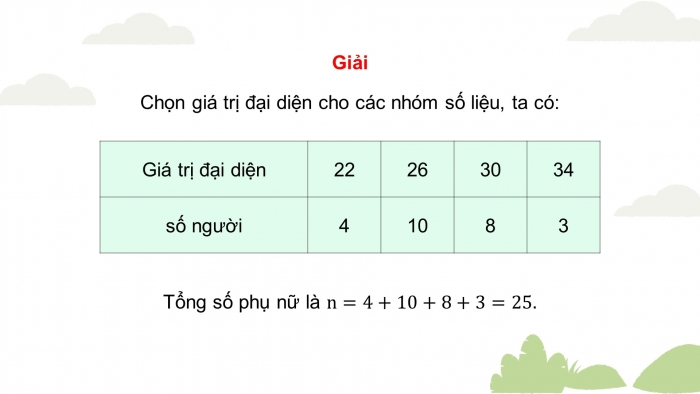
Giải
Chọn giá trị đại diện cho các nhóm số liệu, ta có:
| Giá trị đại diện | 22 | 26 | 30 | 34 |
| số người | 4 | 10 | 8 | 3 |
Tổng số phụ nữ là ![]()
Độ tuổi kết hôn trung bình là:
![]()
Phương sai của mẫu số liệu về độ tuổi kết hôn là:
![]()
Độ lệch chuẩn của mẫu số liệu về độ tuổi kết hôn là:
![]()
Ý nghĩa. Phương sai, độ lệch chuẩn của mẫu số liệu ghép nhóm là các xấp xỉ cho phương sai, độ lệch chuẩn của mẫu số liệu gốc. Chúng được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm xung quanh số trung bình của mẫu số liệu đó. Phương sai, độ lệch chuẩn càng lớn thì mẫu số liệu càng phân tán.
Chú ý. Người ta còn sử dụng các đại lượng sau để đo mức độ phân tán của mẫu số liệu ghép nhóm:
![]()
2. Sử dụng phương sai, độ lệch chuẩn đo độ rủi ro
Trong tài chính, người ta có nhiều cách để đo độ rủi ro của một phương án đầu tư. Một trong các cách đó là sử dụng độ lệch chuẩn của lợi nhuận thu được theo phương án đầu tư. Độ lệch chuẩn càng lớn thì phương án đầu tư càng rủi ro.
Ví dụ: Ông A đầu từ số tiền bằng nhau vào hai lĩnh vực kinh doanh X, Y. Ông A thống kê số tiền thu được mỗi tháng trong vòng 5 năm theo mỗi lĩnh vực cho kết quả như sau:
| Số tiền (triệu đồng) | [10; 15) | [15; 20) | [20; 25) | [25; 30) |
| Số tháng đầu tư vào lĩnh vực X | 10 | 20 | 20 | 10 |
| Số tháng đầu tư vào lĩnh vực Y | 20 | 10 | 10 | 20 |
So sánh giá trị trung bình và độ lệch chuẩn của số tiền thu được mỗi tháng khi đầu tư vào mỗi lĩnh vực X và Y. Đầu tư vào lĩnh vực nào “rủi ro” hơn?
Giải
Chọn giá trị đại diện cho các nhóm số liệu, ta có:
| Giá trị đại diện | 12,5 | 17,5 | 22,5 | 27,5 |
| Số tháng đầu tư vào lĩnh vực X | 10 | 20 | 20 | 10 |
| Số tháng đầu tư vào lĩnh vực Y | 20 | 10 | 10 | 20 |
Số tiền trung bình thu được khi đầu tư vào các lĩnh vực X và Y tương ứng là:
![]()
![]()
![]()
![]()
Như vậy, về trung bình đầu tư vào các lĩnh vực X và Y số tiền được hàng tháng như nhau. Độ lệch chuẩn của số tiền thu được hàng tháng khi đầu tư vào các lĩnh vực X và Y tương ứng là:


Như vậy, độ lệch chuẩn của mẫu số liệu về số tiền thu được hàng tháng khi đầu tư vào lĩnh vực Y cao hơn khi đầu tư vào lĩnh vực X. Người ta nói rằng, đầu tư vào lĩnh vực Y là “rủi ro” hơn.
PHIẾU BÀI TẬP SỐ 1
DẠNG 1: Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm
--------------- Còn tiếp ---------------
Powerpoint dạy thêm Toán 12 KNTT, giáo án điện tử dạy thêm Bài 10: Phương sai và độ lệch chuẩn Toán 12 kết nối, giáo án PPT dạy thêm Toán 12 kết nối Bài 10: Phương sai và độ lệch chuẩn
Nâng cấp lên tài khoản VIP để tải tài liệu và dùng thêm được nhiều tiện ích khác
