Giải luyện tập 2 trang 118 sgk Toán 8 tập 1 CD

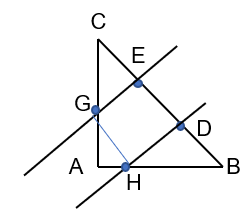
Xét 2 tam giác vuông GEC và HDB có:

• EC = DB (gt)
• $\widehat{C}=\widehat{B}$ (ABC là tam giác vuông cân tại A )

=>2 tam giác vuông GEC và HDB bằng nhau theo trường hợp cạnh góc vuông - góc nhon

=> GE = HD, GC = HB (1)

Tam gác ABC vuông cân tại A nên $\widehat{C}=\widehat{B}$ = $45^{\circ}$

=> Tam giác DBH vuông cân tại D. suy ra:

• DH = DB => GE = DB = DE (2)
• $\widehat{DHB}=\widehat{DBH}$ = $45^{\circ}$ (3)

Từ (1) GC = HB => GA = AH => tam giác AGH vuông cân tại H => $\widehat{AHG}=\widehat{AGH}$ = $45^{\circ}$ (4)

Từ (3) và (4) =>  $\widehat{GHD}$ = $180^{\circ}$ - $45^{\circ}$ - $45^{\circ}$ = $90^{\circ}$

Xét tứ giác EGHD có: 3 góc vuông $\widehat{GHD}$, $\widehat{HDE}$, $\widehat{DEG}$ nên góc còn lại $\widehat{EGH}$ cũng là góc vuông=>EGHD là hình chữ nhật.  Thêm nữa là có 2 cạnh liền kề GE=ED nên là hình vuông (đpcm)