Giải bài tập 3 trang 119 sgk Toán 8 tập 1 CD
Bài tập 3 trang 119 sgk Toán 8 tập 1 CD: Cho tam giác ABC vuông tại A có đường phân giác AD. Gọi H, K lần lượt là hình chiếu của D trên AB, AC. Chứng minh tứ giác AHDK là hình vuông.
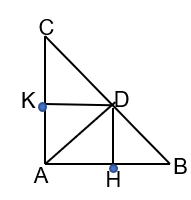
H, K lần lượt là hình chiếu của D trên AB, AC nên $\widehat{DHA}=\widehat{DKA}=90^{\circ}$. Tứ giác AHDK có 3 góc vuông nên góc còn lại cũng là góc vuông. Vậy AHDK là hình chữ nhật.
Xét 2 tam giác vuông DHA và DKA có:
- $\widehat{DAH}=\widehat{DAK} $(AD là đường phân giác của góc A)
- AD chung
=> 2 tam giác vuông DHA và DKA bằng nhau theo trường hợp cạnh huyền, góc nhọn
=> 2 cạnh tương ứng AH = AK. Hình chữ nhật AHDK có 2 cạnh liền kề bằng nhau nên là hình vuông (đpcm)
Xem toàn bộ: Giải toán 8 cánh diều bài 7 Hình vuông

Bình luận