Giải câu 11 bài ôn tập chương 4: Bất đẳng thức, bất phương trình sgk Đại số 10 trang 107

a) Ta có

\(f(x) = {x^4} - {x^2} + 6x - 9 = {\left( {{x^2}} \right)^2} - {\left( {x - 3} \right)^2} = \left( {{x^2} + x - 3} \right)\left( {{x^2} - x + 3} \right)\)

Ta lại có \({{x^2} - x + 3} > 0, ∀x ∈\mathbb R\) ( vì \(a = 1> 0, Δ = 1- 4.3<0\))

\(\Rightarrow f(x)\)cùng dấu với \(x^2+x-3\)

Tam thức \(x^2+x-3\)có hai nghiệm là \(\frac{-1-\sqrt {13}}{2}; \frac{-1+\sqrt {13}}{2}\)

Vậy

• \(f(x)>0\)khi \(x < {{ - 1 - \sqrt {13} } \over 2}\)hoặc \(x > {{ - 1 + \sqrt {13} } \over 2}\)
• \(f(x)<0\)khi \(\frac{-1-\sqrt {13}}{2} < x < \frac{-1+\sqrt {13}}{2}\)

\(g(x) = x^2– 2x -  {4 \over {{x^2} - 2x}}\) 

\(={{{{({x^2} - 2x)}^2} - {2^2}} \over {{x^2} - 2x}}\)

\(= {{({x^2} - 2x + 2)({x^2} - 2x - 2)} \over {{x^2} - 2x}}\)

Ta lại có \(x^2– 2x + 2 > 0 ,∀x ∈\mathbb R\)

\(\Rightarrow g(x)\)cùng dấu với \({{{x^2} - 2x - 2} \over {{x^2} - 2x}}\)

Tam thức \(x^2-2x-2\)có hai nghiệm là \(1-\sqrt 3; 1+\sqrt 3\)

\(x^2-2x\)có hai nghiệm là \(x; 2\)

Ta lập bảng xét dấu

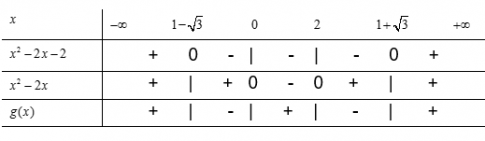
Vậy

• \(g(x)>0\)khi \(x \in \left ( -\infty ;1-\sqrt{3} \right )\cup \left ( 0;2 \right )\cup \left ( 1+\sqrt{3}; +\infty  \right )\)
• \(g(x)>0\)khi \(x \in \left ( 1-\sqrt{3};0 \right )\cup \left ( 2; 1+ \sqrt{3} \right )\)

b) \(x({x^3} - x + 6) > 9 \)

\(\Leftrightarrow {x^4} - {x^2} + 6x - 9 > 0 \)

\(\Leftrightarrow {x^4} - {(x - 3)^2} > 0 \)

\(\Leftrightarrow ({x^2} - x + 3)({x^2} + x - 3) > 0\)

Ta có \({{x^2} - x + 3} > 0, ∀x ∈\mathbb R ( \text{vì} \,\,a = 1> 0, Δ = 1- 4.3<0)\)

\(\Rightarrow  ({x^2} + x - 3) > 0 \Leftrightarrow \left[ \matrix{x < {{ - 1 - \sqrt {13} } \over 2} \hfill \cr x > {{ - 1 + \sqrt {13} } \over 2} \hfill \cr} \right.\)

Vậy nghiệm nguyên của bất phương trình là \(\left\{x\in \mathbb Z|x\le-3\text{ hoặc } x\ge2\right\}\)