Giải câu 11 bài 3: Các hệ thức lượng trong tam giác và giải tam giác
Câu 11: Trang 60 - sgk hình học 10
Muốn đo chiều cao của Tháp Chàm Por Klong Garai ở Ninh Thuận, người ta lấy hai điểm A và B trên mặt đất có khoảng cách AB = 12 m cùng thẳng hàng với chân C của tháp để đặt hai giác kế (hình bên). Chân của giác kế có chiều cao h = 1,3m. Gọi D là đỉnh tháp và hai điểm $A_{1}, B_{1}$ cùng thẳng hàng với $C_{1}$ thuộc chiều cao CD của tháp. Người ta đo được $\widehat{DA_{1}C_{1}}=49^{\circ}$ và$\widehat{DB_{1}C_{1}}=35^{\circ}$. Tính chiều cao CD của tháp đó.
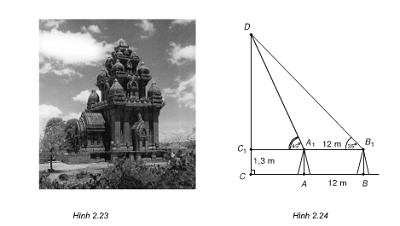
Ta có: $A_{1}B_{1} = AB = 12 m$
Xét $ΔDC_{1}A_{1}$ có: $C_{1}A_{1} = C_{1}D.\cot 49^{\circ}$
Xét $ΔDC_{1}B_{1}$ có: $C_{1}B_{1} = C_{1}D.\cot 35^{\circ}$
Mà $A_{1}B_{1} = C_{1}B_{1} - C_{1}A_{1} = C_{1}D.\cot 35^{\circ} - C_{1}D.\cot 49^{\circ}$
<=> $A_{1}B_{1} = C_{1}D.( \cot 35^{\circ} - \cot 49^{\circ})$
=> $C_{1}D=\frac{A_{1}B_{1}}{\cot 35^{\circ} - \cot 49^{\circ}}\approx 21,47 (m)$
=> Chiều cao CD của tháp là: $CD = 1,3 + 21,47 = 22,77 m$

Bình luận