A. TÓM TẮT LÝ THUYẾT

1. Phương trình đường tròn có tâm và bán kính cho trước

Phương trình đường tròn có tâm \(I(a; b)\,\ \) bán kính \(R\) là:

    ${(x - a)^2} + {(y - b)^2} = {R^2}$

2. Nhận xét

Phương trình đường tròn  \({(x - a)^2} + {(y - b)^2} = {R^2}\)  có thể được viết dưới dạng:

                             $${x^2} + {y^2} - 2ax - 2by + c = 0$$

trong đó \(c = {a^2} + {b^2} + {R^2}\)

Ngược lại, phương trình \({x^2} + {y^2} - 2ax - 2by + c = 0\) là phương trình của đường tròn \((C)\) khi và chỉ khi \({a^2} + {b^2}-c>0\). Khi đó đường tròn \((C)\) có tâm  \(I(a; b)\) và bán kính \(R = \sqrt{a^{2}+b^{2} - c}\)

3. Phương trình tiếp tuyến của đường tròn

Cho điểm \({M_0}({x_0};{y_0})\) nằm trên đường tròn \((C)\) tâm \(I(a; b)\). Gọi \(∆\) là tiếp tuyến với \((C)\) tại \(M_0\).

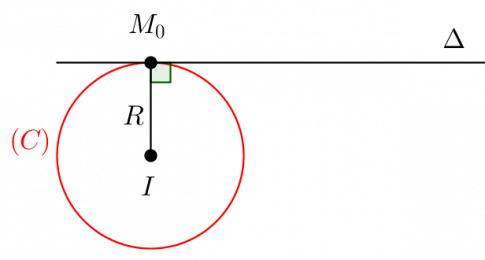
Ta có \(M_0\) thuộc \(∆\) và vectơ \(\vec{IM_{0}}=({x_0} - a;{y_0} - b)\) là vectơ  pháp tuyến cuả \( ∆\).

Do đó  \(∆\) có phương trình là :  $({x_0} - a)(x - {x_0}) + ({y_0} - b)(y - {y_0}) = 0\,\ (1)$

Phương trình (1) là phương trình tiếp tuyến của đường tròn \({(x - a)^2} + {(y - b)^2} = {R^2}\)  tại điểm \(M_0\) nằm trên đường tròn.