A. TÓM TẮT LÝ THUYẾT

1. Định nghĩa đường elip

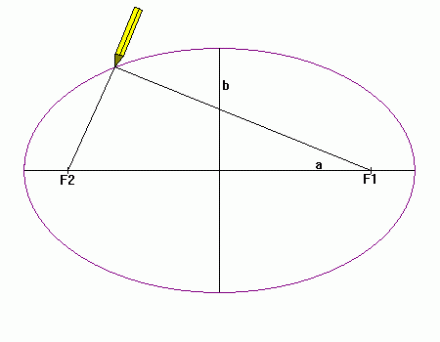
Định nghĩa: Trong mặt phẳng, cho hai điểm cố định \(F_1\) và \(F_2\)

Elip là tập hợp các điểm \(M\) sao cho tổng \(F_1M +F_2M = 2a\) không đổi.

Các điểm \(F_1\) và \(F_2\)  gọi là tiêu điểm của elip.

Khoảng cách \(F_1F_2= 2c\) gọi là tiêu cự của elip.

2. Phương trình chính tắc của elip

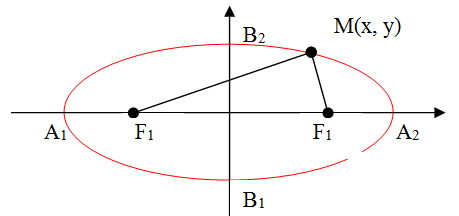
Cho elip có tiêu điểm \(F_1\) và \(F_2\)  chọn hệ trục tọa độ \(Oxy\) sao cho \(F_1(-c ; 0)\) và \(F_2(c ; 0)\). Khi đó người ta chứng minh được:

\(M(x ; y) \in\) elip  \(\Rightarrow\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}} = 1\) (1)

trong đó:   \(b^2= a^2– c^2\)

Phương trình (1) gọi là phương trình chính tắc của elip

3. Hình dạng của elip

Xét elip \((E)\) có phương trình (1):

a) Nếu điểm \(M(x; y)\) thuộc \((E)\) thì các điểm  \(M_1(-x ; y) M_2(x ;- y)\)  và \(M_3(-x ; -y)\) cũng thuộc \((E)\).

Vậy \((E)\) có các trục đối xứng là \(Ox, Oy\) và có tâm đối xứng là gốc \(O\).

b) Thay \(y = 0\)  vào (1) ta có \(x = ±a\) suy ra \((E)\) cắt \(Ox\) tại hai điểm \(A_1(-a ; 0) A_2(a ;0)\).

Tương tự thay \(x = 0\) vào (1) ta được \(y =  ±b\), vậy \((E)\) cắt \(Oy\) tại hai điểm \( B_1(0 ; -b) B_2(0 ;b)\).

Các điểm  \(A_1, A_2, B_1, B_2\) gọi là các đỉnh của elip

Đoạn thẳng  \(A_1A_2\)  gọi là trục lớn, đoạn thẳng \(B_1,B_2\)  gọi là trục nhỏ của elip.

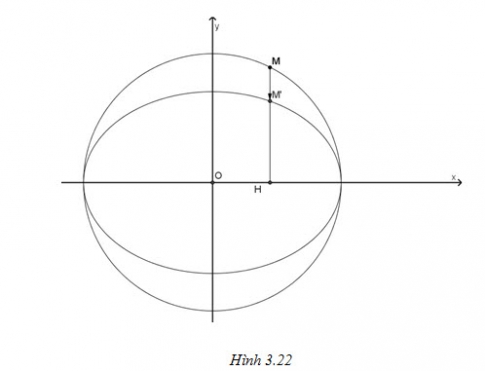
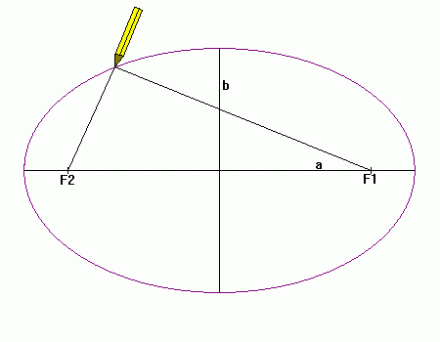
4. Liên hệ giữa đường tròn và đường elip

Nếu tiêu cự của elip càng nhỏ thì $b$ càng gần $a$, tức là trục nhỏ của elip càng gần bằng trục lớn. Lúc đó elip có dạng gần như hình tròn.