Giải bài 3: Các hệ thức lượng trong tam giác và giải tam giác
Bài học giới thiệu nội dung: Các hệ thức lượng trong tam giác và giải tam giác . Một kiến thức không quá khó song đòi hỏi các bạn học sinh cần nắm được phương pháp để giải quyết các bài toán. Dựa vào cấu trúc SGK toán lớp 10, Tech12h sẽ tóm tắt lại hệ thống lý thuyết và hướng dẫn giải các bài tập 1 cách chi tiết, dễ hiểu. Hi vọng rằng, đây sẽ là tài liệu hữu ích giúp các em học tập tốt hơn
A. Tổng hợp kiến thức
1. Định lí Côsin
- Trong tam giác ABC bất kì với $BC = a ; CA=b ; AB =c$, ta có:
$a^{2}=b^{2}+c^{2}-2bc\cos A$ $b^{2}=a^{2}+c^{2}-2ac\cos B$ $c^{2}=a^{2}+b^{2}-2ab\cos C$ |
Hệ quả
$\cos A=\frac{b^{2}+c^{2}-a^{2}}{2bc}$ $\cos B=\frac{a^{2}+c^{2}-b^{2}}{2ac}$ $\cos C=\frac{a^{2}+b^{2}-c^{2}}{2ab}$ |
2. Định lí sin
- Trong tam giác ABC bất kì với $BC = a ; CA=b ; AB =c$, R là bán kính đường tròn ngoại tiếp ,ta có:
| $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$ |
3. Công thức tính diện tích tam giác
- Cho tam giác ABC bất kì với $BC = a ; CA=b ; AB =c$, R và r lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp tam giác ; $p=\frac{a+b+c}{2}$ là nửa chu vi tam giác , ta có :
$S=\frac{1}{2}ab\sin C=\frac{1}{2}bc\sin A=\frac{1}{2}ac\cos B$ $S=\frac{abc}{4R}$ $S=p.r$ $S=\sqrt{p(p-a)(p-b)(p-c)}$ - công thức Hê-rông |
Đặc biệt:
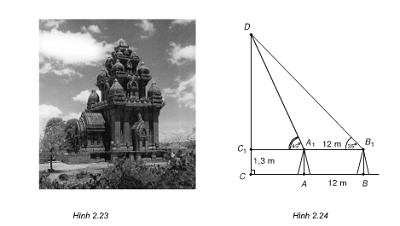
- Dựa vào hệ thức lượng trong tam giác , ta có thể áp dụng để giải tam giác cũng như việc đo đạc ở thực tế.
Nội dung quan tâm khác
Giải bài tập những môn khác
Giải SGK 10 KNTT
Giải SGK 10 CTST
Giải SGK 10 Cánh diều
Giải SBT lớp 10 kết nối tri thức
Giải SBT lớp 10 chân trời sáng tạo
Giải SBT lớp 10 Cánh diều
Giải chuyên đề học tập 10 Kết nối tri thức
Giải chuyên đề học tập 10 Chân trời sáng tạo
Giải chuyên đề học tập 10 Cánh diều
Trắc nghiệm 10 Kết nối tri thức
Trắc nghiệm 10 Chân trời sáng tạo
Trắc nghiệm 10 Cánh diều
Bình luận