Giải bài tập 58 trang 90 SBT toán 10 tập 2 cánh diều
58. Trong mặt phẳng tọa độ Oxy, cho điểm M(1; 1) và đường thẳng ∆: 3x + 4y + 3 = 0. Viết phương trình đường tròn (C), biết (C) có tâm M và đường thẳng ∆ cắt (C) tại hai điểm N, P thỏa mãn tam giác MNP đều.
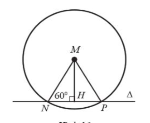
Gọi H là hình chiếu của M lên Δ
Suy ra MH là khoảng cách từ M đến Δ
MH = $\frac{3\times 1+4\times 1+3}{\sqrt{3^{2}+4^{2}}}=2$
Xét tam giác MNH vuông tại H có:
MN =$\frac{MH}{sin60^{\circ}}=\frac{4}{\sqrt{3}}$
Mà R = MN = $\frac{4}{\sqrt{3}}$
Phương trình đường tròn là: $(x-1)^{2}+(y-1)^{2}=\frac{16}{3}$
Giải những bài tập khác
Giải bài tập những môn khác
Giải SGK 10 KNTT
Giải SGK 10 CTST
Giải SGK 10 Cánh diều
Giải SBT lớp 10 kết nối tri thức
Giải SBT lớp 10 chân trời sáng tạo
Giải SBT lớp 10 Cánh diều
Giải chuyên đề học tập 10 Kết nối tri thức
Giải chuyên đề học tập 10 Chân trời sáng tạo
Giải chuyên đề học tập 10 Cánh diều
Trắc nghiệm 10 Kết nối tri thức
Trắc nghiệm 10 Chân trời sáng tạo
Trắc nghiệm 10 Cánh diều
Bình luận