Giải bài tập 10 trang 23 SBT toán 10 tập 2 chân trời
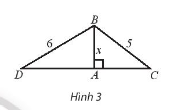
Bài tập 10. Cho tam giác ABC và ABD cùng vuông tại A như Hình 3 có AB = x, BC = 5 và BD 6.
a) Biểu diễn độ đài cạnh AC và AD theo x.
b) Tìm x để chu vi của tam giác ABC là 12.
c) Tìm x để AD = 2AC.
Trả lời:
Vì x là độ dài của cạnh AB nên x > 0
a) AC = $\sqrt{BC^{2} - AB^{2}} = \sqrt{25 - x^{2}}$
AD = $\sqrt{BD^{2} - AB^{2}} = \sqrt{36 - x^{2}}$
b) Có AB + AC + BC = 12
$\Rightarrow x + 5 + \sqrt{25 - x^{2}} = 12$
$\Rightarrow 25 - x^{2} = (7 - x)^{2}$
$\Rightarrow$ x = 4 hoặc x = 3
Thay lần lượt các giá trị trên vào phương trình AB + AC + BC =12 ta thấy x = 4 hoặc x = 3 thỏa mãn
Vậy x = 4 hoặc x = 3 thì chi vi tam giác ABC là 12
c) Giải phương trình AD = 2AC
$\sqrt{36 - x^{2}} = 2\sqrt{25 - x^{2}}$
$\Rightarrow x = -\frac{8\sqrt{3}}{3}$ hoặc $x = \frac{8\sqrt{3}}{3}$
Thay lần lượt các giá trị trên vào phương trình AD = 2AC ta thấy $x = -\frac{8\sqrt{3}}{3}$ hoặc $x = \frac{8\sqrt{3}}{3}$ thỏa mãn
Vì x > 0 nên $x = \frac{8\sqrt{3}}{3}$
Xem toàn bộ: Giải SBT toán 10 chân trời Bài tập cuối chương VII

Bình luận