Bài tập file word mức độ vận dụng cao bài 16: Đường trung bình của tam giác

Câu 1: 

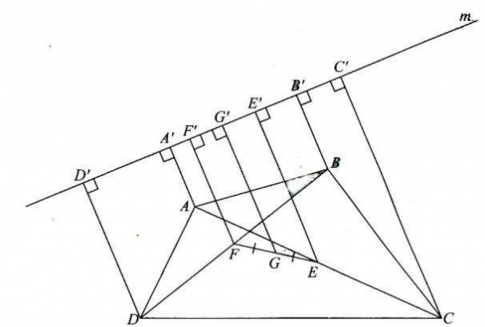
Gọi E và F lần lượt là trung điểm của AC và BD; E' và F' lần lượt là hình chiếu của E, F trên đường thẳng m. Khi đó, GG' là đường trung bình của hình thang EE'F'F

$\Rightarrow GG'=\frac{1}{2}(EE'+FF')$

Mà EE' và FF' lần lượt là đường trung bình của hình thang AA'C'C và BB'D'D.

$\Rightarrow EE'=\frac{1}{2}(AA'+CC')$ và $\Rightarrow FF'=\frac{1}{2}(BB'+DD')$

Thay vào (1) ta được ĐPCM.

Câu 2.

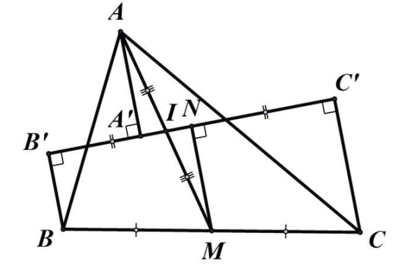
Gọi N là hình chiếu của M trên d.

Xét tứ giác BB'CC' có BB' // CC' (cùng vuông góc d)

=> BBCC' là hình thang.

M là trung điểm BC và MN // BB' // CC' (cùng vuông góc d)

=> MN là đường trung bình của hình thang BBCC'

=> BB' + CC' = 2MN (1)

Chứng minh được

=> AA' = MN  (2)

Từ (1); (2) suy ra BB' + CC' = 2AA'