Bài tập file word mức độ nhận biết bài 16: Đường trung bình của tam giác
1. NHẬN BIẾT (7 câu)
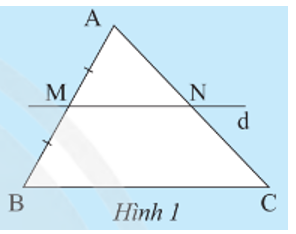
Câu 1: Cho tam giác ABC, vẽ đường thẳng d đi qua trung điểm M của cạnh AB, song song với cạnh BC và cắt AC tại N (Hình 1). Hãy chứng minh N là trung điểm của AC
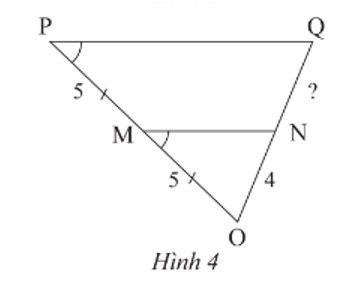
Câu 2: Tìm độ dài đoạn thẳng NQ trong Hình 4
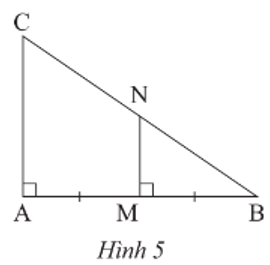
Câu 3: Trong Hình 5, chứng minh MN là đường trung bình của tam giác ABC
Câu 4: Cho M, N lần lượt là trung điểm của hai cạnh AB và AC của tam giác ABC.
a) Tính các tỉ số
b) Chứng minh MN // BC
c) Chứng minh

Câu 5. Tính độ dài đoạn PQ (Hình 10)

Câu 6. Cho MN là đường trung bình của mỗi tam giác ABC trong Hình 9. Hãy tìm giá trị x trong mỗi hình

Câu 7. Cho tam giác ABC cân tại A, có M là trung điểm của BC. Kẻ tií Mx song song với AC cắt AB tại E và tia My song song với AB cắt AC tại F. Chứng minh: a) EF là đường trung bình của tam giác ABC; b) AM là đường trung trực của EF.
Câu 1:
Xét tam giác ABC có MN // BC, theo định lí Thales ta có:
$\frac{AM}{AB}=\frac{AN}{AC}=\frac{1}{2}$
Suy ra N là trung điểm của AC
Câu 2:
Ta có $\widehat{OPQ}=\widehat{OMN}$ mà hai góc này ở vị trí đồng vị nên MN // PQ
Xét tam giác OPQ ta có: MN//PQ, M là trung điểm OP suy ra MN là đường trung bình tam giác OPQ
⇒ N là trung điểm OQ ⇒NQ = ON = 4
Câu 3:
Ta có: MN⊥AB, AC⊥AB nên MN // AC
Xét tam giác ABC có: MN // AC, M là trung điểm AB suy ra MN là đường trung bình tam giác ABC
Câu 4:
a) Vì M là trung điểm AB suy ra $\frac{AM}{AB}=\frac{1}{2}$
Tương tự, $\frac{AN}{AC}=\frac{1}{2}$
b) Xét tam giác ABC có: $\frac{AM}{AB}=\frac{AN}{AC}$ theo định lí Thales đảo ta có: MN // BC
c) Xét tam giác ABC có MN // BC, áp dụng hệ quả định lí Thales, ta có:
$\frac{MN}{BC}=\frac{AM}{AB}=\frac{1}{2}$
Câu 5.
Xét tam giác ABC có: AP = PB = 8cm; AQ = QC = 7 cm suy ra PQ là đường trung bình tam giác ABC nên $PQ=\frac{1}{2}BC=\frac{1}{2}.9=4,5$ (cm)
Câu 6.
a) Xét tam giác ABC có MN là đường trung bình ta có: BC = 2 MN suy ra x = 12
b) Xét tam giác ABC có MN là đường trung bình ta có: BC = 2MN suy ra 2x + 3 = 14 suy ra x = $\frac{11}{2}$
c) Xét tam giác ABC có MN là đường trung bình ta có:
BC = 2MN suy ra 58=2(5x−1)⇒58=10x−2⇒x=6
Câu 7.
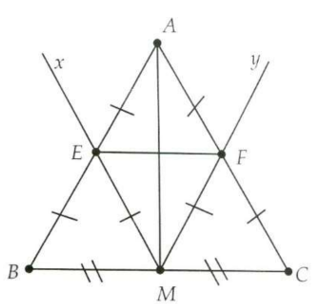
a) Mx đi qua trung điểm M của BC và song song với AC.
Suy ra Mx đi qua trung điểm E của AB (theo Định lí 1).
Tương tự, ta được F cũng là trung điểm của AC.
Khi đó EF trở thành đường trung bình của tam giác ABC;
b) Do ME và MF cũng là đường trung bình nên có ME = MF = AE = AF.
Suy ra AM là đường trung trực của EF.

Bình luận