Bài tập file word mức độ thông hiểu bài 16: Đường trung bình của tam giác
2. THÔNG HIỂU (5 câu)
Câu 1. Cho tam giác ABC vuông tại A, kẻ đường cao AH. Từ H kẻ tia Hx vuông góc với AB tại P và tia Hy vuông góc vói AC tại Q. Trên các tia Hx, Hy lần lượt lấy các điếm D và E sao cho PH = PD, QH = QE. Chứng minh:
a) A là trung điểm của DE;
b) $PQ=\frac{1}{2}DE$
c) PQ = AH.
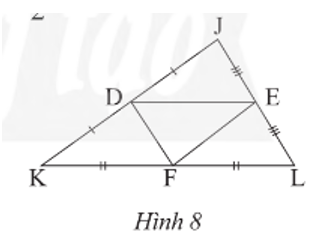
Câu 2. Trong Hình 8, cho biết JK = 10 cm, DE = 6.5 cm, EL = 3.7 cm. Tính DJ, EF, DF, KL
Câu 3: Cho biết cạnh mỗi ô vuông bằng 1 cm. Tính độ dài các đoạn PQ, PR, RQ, AB, BC, CA trong Hình 11

Câu 4: Cho hình thang ABCD (AB //CD) có E và F lần lượt là trung điểm hai cạnh bên AD và BC. Gọi K là giao điểm của AF và DC (Hình 12).
a) Tam giác FBA và tam giác FCK có bằng nhau không? Vì sao?
b) Chứng minh EF // CD // AB
c) Chứng minh $EF=\frac{AB+CD}{2}$

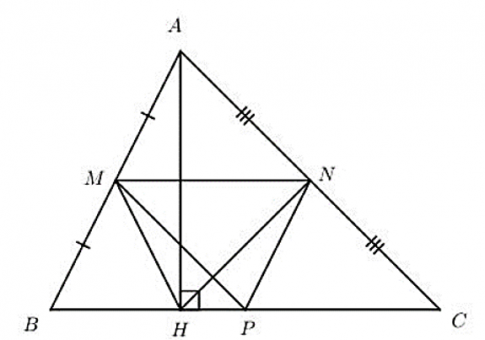
Câu 5: Cho tam giác ABC nhọn. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Kẻ đường cao AH. Chứng minh rằng tứ giác MNPH là hình thang cân.
Câu 1.
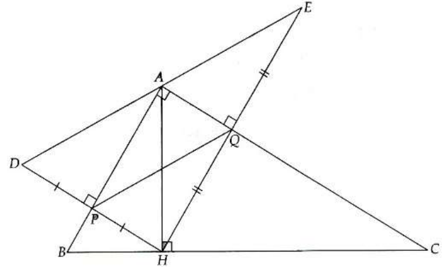
a) Chứng minh được tam giác ADH và AEH cân tại A.
Khi đó: $\widehat{DAP}=\widehat{HAP},\widehat{EAQ}=\widehat{HAQ}$ và AD = AH = AE.
Từ đó, suy ra được A, D, E thẳng hàng và A là trung điểm DE.
b) PQ là đường trung bình của tam giác DHE => ĐPCM.
c) Có AH = AD = AE = 1 2 DE, mà $PQ=\frac{1}{2}DE\Rightarrow$ AH = PQ.
Câu 2.
D là trung điểm của JK suy ra $DJ=\frac{1}{2}JK.10=5$
E là trung điểm của JL suy ra JL = 2EL = 2 . 3,7 = 7,4 (cm)
Trong tam giác JKL có D, E lần lượt là trung điểm của JK và JL suy ra DE là đường trung bình của tam giác JKL suy ra KL = 2DE = 2 . 6,5 = 13 (cm)
Tương tự, ta có: EF là đường trung bình của tam giác JKL
suy ra $EF=\frac{1}{2}JK=\frac{1}{2}.10=5$(cm)
DF là đường trung bình tam giác JKL
Suy ra DF = $DF=\frac{1}{2}JL=\frac{1}{2}.7,4=3,7$ cm.
Câu 3:
Ta có: $AB=\sqrt{2^{2}+4^{2}}=2\sqrt{5}$
$AC=\sqrt{2^{2}+4^{2}}=2\sqrt{5}$
$BC=\sqrt{2^{2}+6^{2}}=2\sqrt{10}$
Xét tam giác ABC có:
P, Q lần lượt là trung điểm của BC và AC
suy ra PQ là đường trung bình tam giác ABC nên $PQ=\frac{1}{2}AB=\frac{1}{2}.2\sqrt{5}=\sqrt{5}$
Tương tự: $PR=\frac{1}{2}AC=\frac{1}{2}.2\sqrt{5}=\sqrt{5}$
$RQ=\frac{1}{2}BC=\frac{1}{2}\times2\sqrt{10}$
Câu 4:
a) Xét tam giác FBA và FCK ta có:
$\widehat{F_{1}}=\widehat{F_{2}}$ (hai góc đối đỉnh)
FB = FC (gt)
$\widehat{FBA}=\widehat{FCK}$ (AB // CD, hai góc so le trong)
Suy ra
b) $\Delta FBA=\Delta FCK$ suy ra FA = FK
Xét tam giác ADK có: EA = ED, FA = FK, suy ra EF là đường trng bình tam giác ABC nên EF // DK
Mà AB // CD suy ra EF//CD//AB
c) EF là đường trung bình tam giác ADK suy ra
$EF=\frac{1}{2}DK=\frac{1}{2}(CD+CK)$
Mà CK = BA (do $$\Delta FBA=\Delta FCK ) nên $EF=\frac{AB+CD}{2}$
Câu 5:
Xét tam giác ABC ta có:
M là trung điểm của AB (gt) ;
N là trung điểm của AC (gt) ;
⇒ MN là đường trung bình của tam giác ABC ⇒MN//BC
⇒ Tứ giác MNPH là hình thang.
Xét tam giác ABC ta có
M là trung điểm của AB (gt) ;
P là trung điểm của BC
⇒MP là đường trung bình của tam giác ABC ⇒ $MP=\frac{1}{2}AC$
ΔACH vuông tại H có HN là trung tuyến (N là trung điểm của AC)⇒NH=12AC. Mà MP=12AC(cmt)
⇒NH=MP
Hình thang MNPH (MN//PH) có MP=NH nên là hình thang cân.

Bình luận