Câu hỏi tự luận mức độ vận dụng cao Toán 12 ctst Bài 2: Công thức xác suất toàn phần và công thức Bayes
4. VẬN DỤNG CAO (4 CÂU)
Câu 1: Một kho hàng có ![]() sản phẩm loại I và
sản phẩm loại I và ![]() sản phẩm loại II, trong đó có
sản phẩm loại II, trong đó có ![]() sản phẩm loại I bị hỏng,
sản phẩm loại I bị hỏng, ![]() sản phẩm loại II bị hỏng. Các sản phẩm có kích thước và hình dạng như nhau. Một khách hàng chọn ngẫu nhiên 1 sản phẩm. Xét các biến cố:
sản phẩm loại II bị hỏng. Các sản phẩm có kích thước và hình dạng như nhau. Một khách hàng chọn ngẫu nhiên 1 sản phẩm. Xét các biến cố:
![]() : "Khách hàng chọn được sản phẩm loại I ";
: "Khách hàng chọn được sản phẩm loại I ";
![]() : "Khách hàng chọn được sản phẩm không bị hỏng".
: "Khách hàng chọn được sản phẩm không bị hỏng".
Tính ![]() .
.
Câu 2: Một cửa hàng có hai loại bóng đèn Led, trong đó có ![]() bóng đèn Led là màu trắng và
bóng đèn Led là màu trắng và ![]() bóng đèn Led là màu xanh, các bóng đèn có kích thước như nhau. Các bóng đèn Led màu trắng có tỉ lệ hỏng là
bóng đèn Led là màu xanh, các bóng đèn có kích thước như nhau. Các bóng đèn Led màu trắng có tỉ lệ hỏng là ![]() và các bóng đèn Led màu xanh có tỉ lệ hỏng là
và các bóng đèn Led màu xanh có tỉ lệ hỏng là ![]() . Một khách hàng chọn mua ngấu nhiên 1 bóng đèn Led từ cửa hàng. Xét các biến cố:
. Một khách hàng chọn mua ngấu nhiên 1 bóng đèn Led từ cửa hàng. Xét các biến cố:
![]() : "Khách hàng chọn được bóng đèn Led màu trắng";
: "Khách hàng chọn được bóng đèn Led màu trắng";
![]() : "Khách hàng chọn được bóng đèn Led không hỏng".
: "Khách hàng chọn được bóng đèn Led không hỏng".
Tính:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Câu 3: Trong một hộp có 10 quả bóng màu xanh và 12 quả bóng màu đỏ, các quả bóng có khối lượng và kích thước như nhau. Bạn Tuấn lấy ngẫu nhiên lần lượt 2 quả bóng, mỗi lần lấy 1 quả và không hoàn lại. Xét các biến cố:
![]() : "Lần thứ nhất lấy được quả bóng màu xanh";
: "Lần thứ nhất lấy được quả bóng màu xanh";
![]() : "Lần thứ hai lấy được quả bóng màu xanh".
: "Lần thứ hai lấy được quả bóng màu xanh".
Tính P(B).
Câu 4: Trong một đợt kiểm tra sức khoẻ, có một loại bệnh X mà tỉ lệ người mắc bệnh là 0,2% và một loại xét nghiệm Y mà ai mắc bệnh X khi xét nghiệm Y cũng có phản ứng dương tính. Tuy nhiên, có 6% những người không bị bệnh X lại có phản ứng dương tính với xét nghiệm Y. Chọn ngẫu nhiên 1 người trong đợt kiểm tra sức khoẻ đó. Giả sử người đó có phản ứng dương tính với xét nghiệm Y. Xác suất người đó bị mắc bệnh X là bao nhiêu (làm tròn kết quà đến hàng phần trăm)?
Câu 1:
Ta có:
![]()
![]()
![]()
Theo công thức xác suất toàn phần, ta có:
![]()
![]()
Theo công thức Bayes, ta có: ![]() .
.
Câu 2:
Ta có:
![]()
![]() ;
;
![]()
Theo công thức xác suất toàn phần, ta có:
![]()
![]() .
.
Câu 3:
Ta có: ![]()
Nếu lần thứ nhất lấy được quả bóng màu xanh thì còn lại 21 quả bóng, trong đó có 9 quả bóng màu xanh, suy ra ![]()
Nếu lần thứ nhất lấy được quả bóng màu đỏ thì còn lại 21 quả bóng, trong đó có 10 quả bóng màu xanh, suy ra ![]() .
.
Theo công thức xác suất toàn phần, ta có:
![]() .
.
Câu 4:
Xét các biến cố:
A: “Người được chọn mắc bệnh X”;
B: “Người được chọn có phản ứng dương tính với xét nghiệm Y”.
Theo giả thiết ta có: ![]() ;
;
![]()
Theo công thức Bayes, ta có:
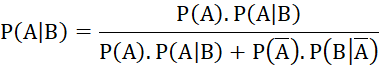
![]()
Vậy nếu người được chọn có phản ứng dương tính với xét nghiệm Y thì xác suất bị mắc bệnh X của người đó là khoảng 0,03.
Giải những bài tập khác
Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều

Bình luận