CHƯƠNG IV: VECTƠ

BÀI 7. CÁC KHÁI NIỆM MỞ ĐẦU

1. KHÁI NIỆM VECTƠ

HĐ1: 

Gọi điểm mà tàu rẽ là C, khi đó:

AC = CB = 10 km.

Suy ra tam giác ACB vuông cân tại C.

Từ đó, $\widehat{CAB}$=$\widehat{CBA}$=45$^{\circ}$ và 

AB = AC$\sqrt{2}$≈14,14km.

Vậy khi tàu chạy thẳng từ A tới B (không đổi hướng), thì tàu phải đi theo hướng S45$^{\circ}$Evà phải đi 14,14 km.

Khái niệm:

Vectơ là một đoạn thẳng có hướng, nghĩa là, trong hai điểm mút của đoạn thẳng, đã chỉ rõ điểm đầu, điểm cuối.

Độ dài của vectơ là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.

Chú ý: 

+ Vectơ có điểm đầu A và điểm cuối B kí hiệu là AB 

+ Vectơ còn được kí hiệu là a,b,x,y,...

+ Độ dài của vectơ $\underset{AB}{\rightarrow}$,$\underset{a}{\rightarrow}$ tương ứng được kí hiệu là |$\underset{AB}{\rightarrow}$|,|$\underset{a}{\rightarrow}$|.

Ví dụ 1 (SGK – tr47)

Luyện tập 1:

Các vectơ có độ dài bằng a và có điểm đầu, điểm cuối là các đỉnh của tam giác ABC là:

$\underset{AB}{\rightarrow}$,$\underset{BA}{\rightarrow}$,$\underset{AC}{\rightarrow}$,$\underset{CA}{\rightarrow}$,$\underset{BC}{\rightarrow}$,$\underset{CB}{\rightarrow}$.

2. HAI VECTƠ CÙNG PHƯƠNG, CÙNG HƯỚNG, BẰNG NHAU

HĐ2: 

Nhận xét đúng: a, c.

Kết luận:

- Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó.

- Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.

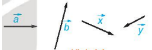
HĐ3: 

Vectơ cùng hướng với vectơ $\underset{a}{\rightarrow}$: $\underset{AB}{\rightarrow}$,$\underset{y}{\rightarrow}$

Vectơ ngược hướng với vectơ $\underset{a}{\rightarrow}$: $\underset{x}{\rightarrow}$,$\underset{z}{\rightarrow}$.

Kết luận:

- Đối với hai vectơ cùng phương thì chúng cùng hướng hoặc ngược hướng.

- Hai vectơ $\underset{a}{\rightarrow}$ và $\underset{b}{\rightarrow}$ được gọi là bằng nhau, kí hiệu $\underset{a}{\rightarrow}$=$\underset{b}{\rightarrow}$, nếu chúng có cùng độ dài và cùng hướng.

Chú ý: 

- Xét các vectơ có điểm đầu và điểm cuối trùng nhau (ví dụ: $\underset{AA}{\rightarrow}$,$\underset{BB}{\rightarrow}$,$\underset{MM}{\rightarrow}$), gọi là vectơ-không.

- Quy ước vectơ không có độ dài bằng 0, cùng hướng, cùng phương với mọi vectơ.

- Các vectơ-không có cùng độ dài và cùng hướng nên bằng nhau và được kí hiệu chung là $\underset{0}{\rightarrow}$.

- Với mỗi điểm O và vectơ $\underset{a}{\rightarrow}$ cho trước, có duy nhất điểm A sao cho $\underset{OA}{\rightarrow}$=$\underset{a}{\rightarrow}$.

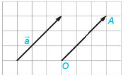
Ví dụ 2 (SGK – tr48)

Luyện tập 2:

+) $\underset{AD}{\rightarrow}$ và $\underset{BC}{\rightarrow}$: độ dài bằng nhau, không cùng phương, không cùng hướng.

+) $\underset{AB}{\rightarrow}$ và $\underset{CD}{\rightarrow}$: độ dài khác nhau, AB < CD, cùng phương, ngược hướng.

+) $\underset{AC}{\rightarrow}$ và $\underset{BD}{\rightarrow}$: độ dài bằng nhau, không cùng phương, không cùng hướng.

Không cặp nào trong các cặp vectơ trên bằng nhau.

Ví dụ 3 (SGK – tr49)

Nhận xét: 

Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi $\underset{AB}{\rightarrow}$,$\underset{AC}{\rightarrow}$cùng phương.

Luyện tập 3:

Đáp án: d.

Chú ý:

Ta có thể dùng vectơ để biểu diễn các đại lượng như lực, vận tốc, gia tốc. Hướng của vectơ chỉ hướng của đại lượng, độ dài của vectơ thể hiện cho độ lớn của đại lượng và được lấy tỉ lệ với độ lớn của đại lượng.

Ví dụ 4 (SGK – tr49)

Vận dụng:

a) Độ lớn của vectơ vận tốc $\underset{v}{\rightarrow}$,$\underset{v_{a}}{\rightarrow}$,$\underset{v_{b}}{\rightarrow}$ tương ứng là 3, 18, 12 (km/h). Do đó tỉ lệ độ dài giữa chúng là: |$\underset{v}{\rightarrow}$||$\underset{v_{a}}{\rightarrow}$||$\underset{v_{b}}{\rightarrow}$| =164 .

b) Do ca nô A chạy xuôi dòng nước nên các vectơ vận tốc $\underset{v}{\rightarrow}$ và $\underset{v_{b}}{\rightarrow}$ cùng phương và ngược hướng.

Vậy trong các vectơ $\underset{v}{\rightarrow}$,$\underset{v_{a}}{\rightarrow}$,$\underset{v_{b}}{\rightarrow}$ có các cặp vectơ cùng phương là:

$\underset{v}{\rightarrow}$ và $\underset{v_{a}}{\rightarrow}$, $\underset{v_{a}}{\rightarrow}$ và $\underset{v_{b}}{\rightarrow}$, $\underset{v_{b}}{\rightarrow}$ và v;

Các cặp vectơ ngược hướng là:

$\underset{v_{a}}{\rightarrow}$ và $\underset{v_{b}}{\rightarrow}$, $\underset{v_{b}}{\rightarrow}$ và $\underset{v}{\rightarrow}$.