CHƯƠNG III. HỆ THỨC LƯỢNG TRONG TAM GIÁC

BÀI 5: GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 0$^{\circ}$ ĐẾN 180$^{\circ}$

1. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC

Khái niệm:

Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O, bán kính R = 1 nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị.

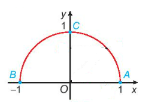
Cho một góc , 0$^{\circ}$≤α≤180$^{\circ}$. Khi đó có duy nhất điểm M(x$_{o}$; y$_{o}$) trên nửa đường tròn đơn vị nói trên để $\widehat{xOM}$=α.

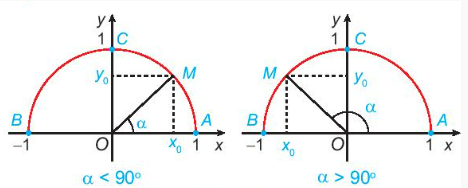
HĐ1: 

a) 

α=90$^{\circ}$: M trùng với điểm C.

α<90$^{\circ}$: M nằm trên cung AC (không trùng điểm C và A).

α>90$^{\circ}$: M nằm trên cung CB (không trùng C và B).

b) coscosα  bằng hoành độ của của điểm M.

sinsinα  bằng tung độ của của điểm M.

Định nghĩa:

Với mỗi góc α(0$^{\circ}$≤180$^{\circ}$), gọi M(xo) là điểm trên nửa đường tròn đơn vị sao cho $\widehat{xOM}$= α. Khi đó:

+ sin của góc là tung độ y$_{o}$ của điểm M, được kí hiệu là sinsinα.

+ côsincủa góc là hoành độ x$_{o}$ của điểm M, được kí hiệu là coscosα.

+ Khi α≠90$^{\circ}$ (hay x$_{o}$≠0), tang  của αlà $\frac{y_{o}}{x_{o}}$, được kí hiệu là tantanα.

+ Khi α≠0$^{\circ}$và α≠180$^{\circ}$ (hay y$_{o}$≠0), côtang của α là $\frac{x_{o}}{y_{o}}$, được kí hiệu là cotcotα.

Chú ý:

tantanα =$\frac{sinsinα}{coscosα}$  (α≠90$^{\circ}$);

cotcotα =$\frac{coscosα}{sinsinα}$  (α≠0$^{\circ}$và α≠180$^{\circ}$);

tantanα =$\frac{1}{cotcotα}$  (α∉{0$^{\circ}$ 90$^{\circ}$ 180$^{\circ}$}).

Bảng giá trị lượng giác của một số góc đặc biệt:

Ví dụ 1 (SGK – tr35)

Luyện tập 1: 

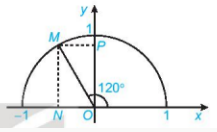
M là điểm nằm trên nửa đường tròn sao cho $\widehat{xOM}$=120$^{\circ}$. GỌi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.

Vì $\widehat{xOM}$=120$^{\circ}$ nên $\widehat{MON}$=60$^{\circ}$,$\widehat{MOP}$=30$^{\circ}$.

Xét tam giác MOP vuông tại P có: 

OP=OM.coscos 30$^{\circ}$=$\frac{\sqrt{3}}{2}$.

MP=OM.sinsin 30$^{\circ}$=$\frac{1}{2}$.

Điểm M nằm bên trái trục tung nên có tọa độ là (-$\frac{1}{2}$;$\frac{\sqrt{3}}{2}$)

Theo định nghĩa có:

sinsin 120$^{\circ}$=-$\frac{1}{2}$; coscos 120$^{\circ}$=-$\frac{1}{2}$

tantan 120$^{\circ}$=-$\sqrt{3}$; cotcot 120$^{\circ}$=-$\frac{\sqrt{3}}{3}$

Chú ý: 

- Khi tìm x biết sin x, máy tính chỉ đưa ra giá trị x≤90$^{\circ}$.

- Muốn tìm x khi biết cos x, tan x, ta cũng làm tương tự như trên, chỉ thay phím tương ứng bới phím 

2. MỐI QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA HAI GÓC BÙ NHAU

Với một góc tùy ý (0$^{\circ}$≤α≤180$^{\circ}$), gọi M, M' là hai điểm trên nửa đường tròn đơn vị tương ứng với hai góc bù nhau và 180$^{\circ}$-α

($\widehat{xOM}$=α,$\widehat{xOM'}$=180$^{\circ}$-α).

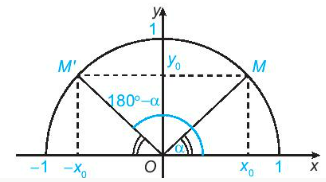
HĐ2: Hai điểm M và M' đối xứng với nhau qua trục Oy.

sinsin ( 180$^{\circ}$-α)=sinsinα

coscos ( 180$^{\circ}$-α)=-coscosα .

Kết luận:

Đối với hai góc bù nhau,α và 180$^{\circ}$-α, ta có:

sinsin( 180$^{\circ}$-α)=sinsinα;

coscos( 180$^{\circ}$-α)=-coscosα;

tantan ( 180$^{\circ}$-α)=-tantan α (α≠90$^{\circ}$);

cotcot ( 180$^{\circ}$-α)=-cotcotα

0$^{\circ}$<α<180$^{\circ}$

Ví dụ 2 (SGK – tr36)

Luyện tập 2:

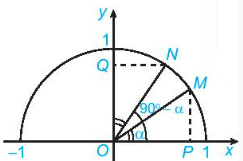
Xét ΔMOP và ΔNOQ có:

$\widehat{OPM}$=$\widehat{OQN}$=90$^{\circ}$

OM = ON
$\widehat{POM}$=$\widehat{QON}$

⇒ΔMOP=ΔNOQ

{OP=OQ MP=NQ

=> coscosα  =sinsin ( 90$^{\circ}$-α).

Vận dụng:

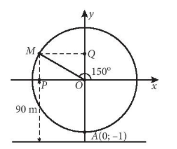
Do mỗi vòng quay, đu quay mất 30 phút nên sau 20 phút, đu quay quay được $\frac{2}{3}$ vòng.

Từ đó $\widehat{xOM}$=$\frac{2}{3}$.360$^{\circ}$-90$^{\circ}$=150$^{\circ}$.

Do đó M có tung độ bằng sinsin 150$^{\circ}$=$\frac{1}{2}$.

Mặt khác, 1 đơn vị trong mặt phẳng tọa độ Oxy ứng với 75 m trong thực tế, nên độ dài đoạn thẳng OQ ứng với $\frac{75}{2}$=37,5 m trong thực tế.

Vậy sau 20 phút quay, đu quay ở độ cao là: 37,5 + 90 = 127, 5 (m).