Lý thuyết trọng tâm toán 10 chân trời bài 2: Hoán vị, chỉnh hợp và tổ hợp
Tổng hợp kiến thức trọng tâm toán 10 chân trời sáng tạo bài 2 Hoán vị, chỉnh hợp và tổ hợp. Tài liệu nhằm củng cố, ôn tập lại nội dung kiến thức bài học cho học sinh dễ nhớ, dễ ôn luyện. Kéo xuống để tham khảo
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
CHƯƠNG VIII. ĐẠI SỐ TỔ HỢP
BÀI 2. HOÁN VỊ, CHỈNH HỢP VÀ TỔ HỢP
1. HOÁN VỊ
HĐKP1:
a) Tất cả các kết quả bốc thăm có thể xảy ra là: A, B, C; A, C, B; B, A, C ; B, C, A; C, A, B ; C, B, A.
b) Từ câu a) => có tất cả 6 kết quả như vậy. Ngoài cách đếm lần lượt từng kết quả, ta có cách sau:
+ CĐ1: Chọn 1 trong 3 đội xếp vào vị trí thứ nhất, có 3 cách chọn.
+ CĐ2: Chọn 1 trong 2 đội còn lại xếp vào vị trí thứ hai, có 2 cách chọn.
+ CĐ3: Xếp đội còn lại vào vị trí thứ ba.
Áp dụng quy tắc nhân có: 3.2.1 = 6 kết quả khác nhau có thể xảy ra.
Kết luận:
- Cho tập hợp A có n phần tử (n≥1).
Mỗi cách sắp xếp n phần tử của A theo một thứ tự gọi là một "hoán vị" các phần tử đó (gọi tắt là hoán vị của A hay n phần tử).
+ Kí hiệu: P$_{n}$ - số hoán vị của n phần tử.
- Số hoán vị của n phần tử (n≥1) bằng:
P$_{n}$ = n.(n-1).(n-2)…2.1
Chú ý:
- Ta đưa vào kí hiệu: n!=nn-1n-2…2.1 và đọc là n giai thừa hoặc giai thừa của n. Khi đó, P$_{n}$ = n!
- Quy ước: 0! = 1
Ví dụ 1: SGK – tr27
Ví dụ 2: SGK – tr27
Thực hành 1:
Mỗi cách sắp xếp 6 thành viên vào 6 ghế ngồi cùng dãy theo thứ tự là một hoán vị của 6 thành viên. Do đó, số cách sắp xếp sáu thành viên vào 6 ghế ngồi là:
P$_{6}$= 6.5.4.3.2.1 = 720 (cách)
Thực hành 2:

Mỗi cách sắp xếp 6 thành viên vào 6 ghế ngồi cùng dãy theo thứ tự là một hoán vị của 6 thành viên. Do đó, số cách sắp xếp sáu thành viên vào 6 ghế ngồi là:
P$_{6}$= 6.5.4.3.2.1 = 720 (cách)
Vận dụng 1:
Mỗi thứ hạng của 14 đội bóng là một hoán vị của 14 đội bóng. Do đó, số khả năng thức hạng các đội bóng khi mùa giải kết thúc là:
P$_{14}$= 14! (cách)
2. CHỈNH HỢP
HĐKP2:

a) Bốn cách chọn và cắm cờ để báo 4 tín hiệu khác nhau là:
Đỏ, xanh, vàng; đỏ, cam, vàng; trắng, vàng, đỏ; xanh, vàng, cam.
b) Chọn 3 lá cờ từ 5 lá cờ và sắp xếp chúng theo thứ tự được gọi là một chỉnh hợp chập 3 của 5 lá cờ. Số các chỉnh hợp chập 3 của 5 lá cờ số các chỉnh hợp này bằng: 5.4.3 = 60.
Vậy có thể báo nhiều nhất 60 tín hiệu khác nhau.
=> Kết luận:
- Cho tập hợp A có n phần tử (n≥1) và số nguyên k với 1 ≤ k ≤n.
Mỗi cách lấy k phần tử của A và sắp sếp chúng theo một thứ tự gọi là một chỉnh hợp chập k của n phần tử đó.
+ Kí hiệu: A$_{n}^{k}$ - số chỉnh hợp chập k của n phần tử (1 ≤ k ≤ n) bằng:
A$_{n}^{k}$ = n.(n-1).(n-2)…(n-k+1) =$\frac{n!}{(n-k)!}$
Nhận xét:
Mỗi hoán vị của n phần tử cũng chính là chỉnh hợp chập n của n phần tử đó.
Ta có: P$_{n}$=A$_{n}^{k}$, n $\leq $ 1.
Ví dụ 3: SGK – tr29
Ví dụ 4: SGK – tr29
Thực hành 2:
a) Chọn 3 chữ số trong 7 chữ số đã cho sao cho 3 chữ số đôi một khác nhau là một chỉnh hợp chập 3 của 7. Do đó, có thể lập được:
A$_{7}^{3}$=7.6.5.4=840 số có ba chữ số đôi một khác nhau.
b)
Chọn chữ số hàng đơn vị là chữ số lẻ. Có 4 cách chọn (chọn 2 hoặc 4)
Chọn 2 trong 6 chữ số còn lại tạo thành hàng chục và hàng đơn vị sao cho đôi một khác nhau là một chỉnh hợp chập 2 của 6 => có A$_{6}^{2}$=6.5.=840
=> Áp dụng quy tắc nhân ta có: 4.30 = 120 số lẻ.
3. TỔ HỢP
HĐKP3:

a. Tất cả các cách Lan có thể chọn 3 cuốn sách từ 4 cuốn sách là:
{A; B; C} hoặc {A; B: D} hoặc {A; C; D) hoặc (B; C; D).
Vậy có tất cả 4 cách.
b. Cách sắp xếp thứ tự đọc trong 3 cuốn đã chọn là một hoán vị của 3 cuốn đó => Có: P$_{3}$ =3! = 6 cách xếp chúng theo thứ tự.
c. Mỗi cách chọn 3 cuốn sách từ 4 cuốn sách và sắp xếp theo thứ tự là một chỉnh hợp chập 3 của 4 phần tử A, B, C, D => Có A$_{4}^{3}$=4!(4-3)!=24 cách.
Kết luận:
- Cho tập hợp A có n phần tử (n≥1)
Mỗi tập con gồm k phần tử (1 ≤ k ≤n ) của A được gọi là một tổ hợp chập k của n phần tử.
Kí hiệu: C$_{n}^{k}$ – số tổ hợp chập k của n phần tử (1 ≤ k ≤n).
Số các tổ hợp chập k của n phần tử (1 ≤ k ≤n) bằng: C$_{n}^{k}$ =$\frac{n!}{k!(n-k)!}$
Chú ý:
Người ta quy ước C$_{n}^{0}$=1
Ví dụ 5: SGK – tr30
Nhận xét:
C$_{n}^{k}$ =C$_{n}^{n-k}$(0≤ k ≤n)
Thực hành 3:
a) C$_{7}^{2}$=$\frac{7!}{2!.5!}$=$\frac{7.6.5!}{2!.5!}$=$\frac{42}{2}$=21
b) C$_{9}^{0}$+C$_{9}^{9}$=$\frac{9!}{0!.(9-0)!}$+$\frac{9!}{9!.(9-9)!}$=1+1=2
c) C$_{15}^{3}$-C$_{14}^{3}$=$\frac{15!}{3!.(15-3)!}$-$\frac{14!}{3!.(14-3)!}$
=$\frac{15.14.13.12!}{3!.12!}$-$\frac{14.13.12.11!}{3!.11!}$
=$\frac{15.14.13-14.13.12}{3!}$=$\frac{14.13.3}{6}$=91
Thực hành 4
a) Mỗi cách chọn 2 đội trong 7 đội tham gia thi đấu là một tổ hợp chập 2 của 7 đội. Do đó, nội dung này có tất cả số trận đấu là:
C$_{7}^{2}$=$\frac{7!}{2!.5!}$=$\frac{7.6.5!}{2!.5!}$=$\frac{42}{2}$=21 (cách)
b) Kết quả 3 đội có thành tích tốt nhất trong 7 đội tham gia thi đấu là một tổ hợp chập 3 của 7 đội. Do đó số khả năng có thể xảy ra về ba đội được chọn đi thi đấu cấp liên trường là:
C$_{6}^{2}$=$\frac{6!}{2!.4!}$=$\frac{6.5.4!}{2!.4!}$=$\frac{6.5}{2!}$=15 (cách)
b) Cách chọn 3 điểm trong 6 điểm đã cho là một tổ hợp chập 3 của 6 điểm. Do đó, số tam giác có đỉnh thuộc các điểm đã cho là:
C$_{6}^{3}$=$\frac{6!}{3!.3!}$=$\frac{6.5.4.3!}{6.3!}$=20 (cách)
Vận dụng 2:
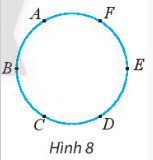
a) Cách chọn 2 điểm trong 6 điểm đã cho là một tổ hợp chập 2 của 6 điểm. Do đó, số đoạn thẳng có điểm đầu mút thuộc các điểm đã cho là:
C$_{6}^{2}$=$\frac{6!}{2!.4!}$=$\frac{6.5.4!}{2!.4!}$=$\frac{6.5}{2!}$=15 (cách)
b) Cách chọn 3 điểm trong 6 điểm đã cho là một tổ hợp chập 3 của 6 điểm. Do đó, số tam giác có đỉnh thuộc các điểm đã cho là:
C$_{6}^{3}$=$\frac{6!}{3!.3!}$=$\frac{6.5.4.3!}{6.3!}$=20 (cách)
4. TÍNH SỐ CÁC HOÁN VỊ, CHỈNH HỢP, TỔ HỢP BẰNG MÁY TÍNH CẦM TAY
Ví dụ 6: SGK-tr31,32
Thực hành 5:
a)

b)

c)
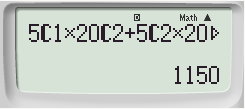
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây

Bình luận