1. NHẬN BIẾT (5 câu)

Câu 1: Viết các đa thức sau dưới dạng tích

a) $8y^{3}+1$

b) $y^{3}-8$

Giải:

a) $8y^{3}+1=(2y)^{3}+13=(2y+1)\left [ (2y)^{2}-2y+12 \right ]=(2y+1)(4y^{2}-2y+1)$

b) $y^{3}-8=y^{3}-23=(y-2)(y^{2}+2y+2^{2})=(y-2)(y^{2}+2y+4)$

Câu 2: Tính

a) $(x+1)(x^{2}-x+1)$

b) $\left ( 2x-\frac{1}{2} \right )(4x^{2}+x+\frac{1}{4})$

Giải:

a) $(x+1)(x^{2}-x+1)=x^{3}+1$

b) $\left ( 2x-\frac{1}{2} \right )(4x^{2}+x+\frac{1}{4})=(2x-\frac{1}{2})\left [ (2x)^{2}+x+(\frac{1}{2})^{2}\right ]=(2x)^{3}-\left ( \frac{1}{2} \right )^{3}=8x^{3}-\frac{1}{8}$

Câu 3: Viết các biểu thức sau thành đa thức

a) $(a-5)(a^{2}+5a+25)$

b) $(x+2y)(x^{2}-2xy+4y^{2})$

Giải:

a) $(a-5)(a^{2}+5a+25)=(a-5)(a^{2}+5a+5^{2})=a^{3}-5^{3}$

b) $(x+2y)(x^{2}-2xy+4y^{2})=(x+2y)(x^{2}-2xy+(2y)^{2})=x^{3}+(2y)^{3}=x^{3}+8y^{3}$

Câu 4: Với a,b là hai số thực bất kì, thực hiện phép tính: 

a) $(a+b)(a^{2}-ab+b^{2})$

b) $(a-b)(a^{2}+ab+b^{2})$

Giải:

a) $(a+b)(a^{2}-ab+b^{2})$

$=a.a^{2}-a.ab+a.b^{2}+b.a^{2}-b.ab+b^{3}$

$=a^{3}-a^{2}b+ab^{2}+a^{2}b-a^{2}b+b^{3}$

$=a^{3}+b^{3}$

b) $(a-b)(a^{2}+ab+b^{2})$

$=a.a^{2}+a.ab+a.b^{2}-b.a^{2}-b.ab-b^{3}$

$=a^{3}+a^{2}b+ab^{2}-a^{2}b-a^{2}b-b^{3}$

$=a^{3}-b^{3}$

Câu 5. Viết mỗi biểu thức sau dưới dạng tích:

a) $27x^{3}+1$

b) $64-8y^{3}$

Giải:

a) $27x^{3}+1=(3x)^{3}+13=(3x+1)((3x)^{2}-3x.1+12)=(3x+1)(9x^{2}-3x+1)$

b) $64-8y^{3}=4^{3}-8y^{3}=(4-8y)\left [ 4^{2} +4.8y+(8y)^{2}\right ]=(4-8y)(16+32y+64y^{2})$

2. THÔNG HIỂU (6 câu)

Câu 1. Chứng minh giá trị của mỗi biểu thức sau không phụ thuộc vào giá trị của biến x. 

a) $E=(x+3)(x^{2}-3x+9)-(x-2)(x^{2}+2x+4)$

b) $G=(2x-1)(4x^{2}+2x+1)-8(x+2)(x^{2}-2x+4)$

Giải:

a) $E=(x+3)(x^{2}-3x+9)-(x-2)(x^{2}+2x+4)$

$=(x+3)(x^{2}-3x+9)-(x-2)(x^{2}+2x+4)$

$=(x.x^{2}-x.3x+9x+3x^{2}-9x+27)-(x.x^{2}+x.2x+4x-2x^{2}-2.2x-2.4)$

$=(x^{3}-3x^{2}+9x+3x^{2}-9x+27)-(x^{3}+2x^{2}+4x-2x^{2}-4x-8)$

$=(x^{3}+27)-(x^{3}-8)$

$=x^{3}+27-x^{3}+8$

=35

Vậy giá trị của biểu thức E luôn luôn bằng 35 với mọi x.

b) $G=(2x-1)(4x^{2}+2x+1)-8(x+2)(x^{2}-2x+4)$

$=(8x^{3}+4x^{2}+2x-4.x^{2}-2x-1)-(8x^{3}-16x^{2}+32x+16x^{2}-32x+64)$

$=(8x^{3}-1)-(8x^{3}+64)$

$=8x^{3}-1-8x^{3}-64$

=-65

Vậy giá trị của biểu thức G luôn luôn bằng -65 với mọi x

Câu 2. Tính nhanh:

a) $18^{3}+2^{3}$

b) $23^{3}-27$

Giải:

 a) $18^{3}+2^{3}$

= $(18+2)^{3}-3.18.2(18+2)$

= $20^{3}-6.18.20$

= 5840

b) $23^{3}-27$

= $(23-3)^{3}+3.23.3.(23-3)$

= $20^{3}+9.23.20$

=12140

Câu 3: Tính giá trị biểu thức:
a,$A=2(x^{3}+y^{3})-3(x^{2}+y^{2})$  biết x+y=1
b)$B=x^{3}+y^{3}+3xy$ biết x+y=1
c,$C=8x^{3}-27y^{3}$ biết xy=4 và 2x-3y=5

Giải:

a) A=-1

b) B=1

c)C=485

Câu 4. Thực hiện phép tính bằng hai cách: $(x + y)^{3}+ (x-2y)^{3}$

Giải:

Cách 1: Ta có:

$(x + y)^{3}+ (x-2y)^{3}$

$=(x+y+x-2y)\left [ (x+y)^{2}-(x+y)(x-2y)+(x-2y)^{2} \right ]$

$=(2x-y)\left [ x^{2}+2xy+y^{2}-x^{2}+2xy-xy+2y^{2}+x^{2} -4xy+4y^{2}\right ]$

$=(2x-y)\left [ x^{2}+7y^{2}-xy \right ]$

$=2x^{3}-3x^{2}y+15xy^{2}-7y^{3}$

Cách 2: Ta có:

$(x + y)^{3}+ (x-2y)^{3}$

$=x^{3}+3x^{2}y+3xy^{2}+y^{3}+x^{3}-6x^{2}y+12xy^{2}-8y^{3}$

$=2x^{3}-3x^{2}y+15xy^{2}-7y^{3}$

Câu 5. Cho x + y = 1. Tính giá trị biểu thức A = $x^{3}+3xy+y^{3}$

Giải:

Ta có:

A = $x^{3}+3xy+y^{3}$

A = $x^{3}+y^{3}+3xy$

A = $(x+y)(x^{2}-xy+y^{2})+3xy$

A = $(x+y)\left [ (x+y)^{2}-3xy \right ]+3xy$

Thay x + y = 1 vào A ta được:

A = $(x+y)\left [ (x+y)^{2}-3xy \right ]+3xy$

A = 1.(1 – 3xy) + 3xy

A = 1 – 3xy + 3xy

A = 1

Vậy A = 1

Câu 6. Cho x - y = 1. Tính giá trị biểu thức A = $x^{3}-3xy-y^{3}$

Giải:

Ta có:

A = $x^{3}-3xy-y^{3}$

A = $x^{3}-y^{3}-3xy$

A = $(x-y)(x^{2}+xy+y^{2})-3xy$

A = $(x-y)\left [ (x-y)^{2} +3xy\right ]-3xy$

Thay x - y = 1 vào A ta được:

A = $(x-y)\left [ (x-y)^{2} +3xy\right ]-3xy$

A = 1.(1 + 3xy) - 3xy

A = 1 + 3xy - 3xy

A = 1

Vậy A = 1

3. VẬN DỤNG (6 câu)

Câu 1: Từ một khối lập phương có cạnh bằng 2x + 1, ta cắt bỏ một khối lập phương có cạnh bằng x + 1 (xem Hình 5). Tính thể tích phần còn lại, viết kết quả dưới dạng đa thức.

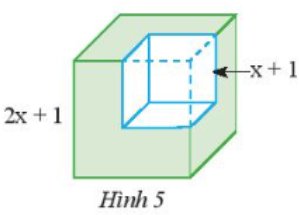
Giải: 

Thể tích phần còn lại:

$(2x+1)^{3}-(x+1)^{3}=\left [ 2x+1-(x+1) \right ]\left [ (2x+1)^{2}+(2x+1)(x+1)-(x+1)^{2} \right ]$

$=(2x+1-x-1)(4x^{2}+4x+1+2x^{2}+2x+x+1-x^{2}-2x-1)$

$=x(5x^{2}+5x+1)=5x^{3}+5x^{2}+x$

Câu 2: 

a) Cho x + y = 5 và xy = 6. Tính $x^{3}+y^{3}$

b) Cho x - y = 3 và xy = 40. Tính $x^{3}-y^{3}$

Giải:

a) $x^{3}+y^{3}=(x+y)(x^{2}-xy+y^{2})=(x+y)\left [ (x^{2}+2xy+y^{2}) -3xy\right ]$

$=(x+y)\left [ (x+y)^{2}-3xy \right ]=5(5^{2}-3\times 6)=35$

b) $x^{3}+y^{3}=(x-y)(x^{2}-xy+y^{2})=(x-y)\left [ (x^{2}-2xy+y^{2}) +3xy\right ]$

$=(x-y)\left [ (x-y)^{2}+3xy \right ]=3(3^{2}+3\times 40)=387$

Câu 3. Cho a+b=S và ab=P. Hãy biểu diễn $B=a^{3}+b^{3}$ theo S và P

Giải:

$B=a^{3}+b^{3}=(a+b).(a^{2}-ab+b^{2})$

$=(a+b).\left [ (a+b)^{2}-3ab \right ]$

$=S.\left [ S^{2} -3P\right ]$

Bài 4. Cho a – b = m; a.b = n. Tính theo m, n giá trị của biểu thức C = $a^{3}-b^{3}$

Giải:

$B=a^{3}-b^{3}=(a-b).(a^{2}+ab+b^{2})$

$=(a-b).\left [ (a-b)^{2} -3ab\right ]$

$=m.(m^{2}+3n)$

Câu 5. Chứng minh rằng:
a) $a^{3}+b^{3}=(a+b)^{3}-3ab(a+b)$
b) $a^{3}-b^{3}=(a-b)^{3}+3ab(a-b)$
Áp dụng: Tính $a^{3}+b^{3}$, biết a.b=6 và a+b=-5

Giải:

a) Biến đổi vế phải ta được:

VP=$a^{3}+b^{3}=(a+b)^{3}-3ab(a+b)$

$a^{3}+3a^{2}b+3ab^{2}+b^{3}-3a^{2}b-3ab^{2}$

$a^{3}+b^{3}=VT$

b) Biến đổi vế phải ta được:

VP=$a^{3}-b^{3}=(a-b)^{3}+3ab(a-b)$

$a^{3}-3a^{2}b+3ab^{2}-b^{3}+3a^{2}b-3ab^{2}=a^{3}-b^{3}=VT$

Kết luận, vậy: $ a^{3}-b^{3}=(a-b)^{3}+3ab(a-b)$

Câu 6. Tìm x, biết: 

$(x-4).(x^{2}+4x+16)+x(x+5)(5-x)=12$

Giải:

$(x-4).(x^{2}+4x+16)+x(x+5)(5-x)=12$

$\Leftrightarrow x^{3}-4^{3}+x(5^{2}-x^{2})=12$

$\Leftrightarrow x^{3}-64+25x-x^{3}=12$

$\Leftrightarrow 25x=76$

$\Leftrightarrow x=\frac{76}{25}$

4. VẬN DỤNG CAO (1 câu)

Câu 1:  Chứng minh rằng: $(x+y+z)^{3}=x^{3}+y^{3}+z^{3}+3.(x+y).(y+z).(z+x)$

Giải:

Xét vế trái có:

$(x+y+z)^{3}$

=$(x+y)^{3}+3(x+y)^{2}z+3(x+y)z^{2}+z^{3}=x^{3}+3x^{2}y+3xy^{2}+y^{3}$