1. NHẬN BIẾT (5 câu)

Câu 1: Tính tổng $P(x)+Q(x)$ và hiệu $P(x)-Q(x)$ biết:

$P(x)=x^{4}+4x^{3}+x^{2}+2x+2$; $Q(x)=x^{4}+x^{3}+2x^{2}+2x+1$

Giải:

+) $P(x)+Q(x)=(x^{4}+4x^{3}+x^{2}+2x+2)+(x^{4}+x^{3}+2x^{2}+2x+1)$

$P(x)+Q(x)=(x^{4}+x^{4})+(4x^{3}+x^{3})+(x^{2}+2x^{2})+(2x+2x)+(2+1)$

$P(x)+Q(x)=2x^{4}+5x^{3}+3x^{2}+4x+3$

+) $P(x)-Q(x)=(x^{4}+4x^{3}+x^{2}+2x+2)-(x^{4}+x^{3}+2x^{2}+2x+1)$

 $P(x)-Q(x)=x^{4}+4x^{3}+x^{2}+2x+2-x^{4}-x^{3}-2x^{2}-2x-1$

$P(x)-Q(x)=(x^{4}-x^{4})+(4x^{3}-x^{3})+(x^{2}-2x^{2})+(2x-2x)+(2-1)$

$P(x)-Q(x)= 3x^{3}-x^{2}+1$

Câu 2: Tính tổng $M(x)+N(x)$ và $M(x)-N(x)$ hiệu biết:

$M(x)=x^{4}+5x^{3}-x^{2}-x+1$; $N(x)=x^{4}+2x^{3}-2x^{2}-3x+2$

Giải:

a) $M(x)+N(x)=(x^{4}+5x^{3}-x^{2}-x+1)+(x^{4}+2x^{3}-2x^{2}-3x+2)$

$M(x)+N(x)=(x^{4}+5x^{3}-x^{2}-x+1)+(x^{4}+2x^{3}-2x^{2}-3x+2)$

$M(x)+N(x)= (x^{4}+x^{4})+(5x^{3}+2x^{3})+(-x^{2}-2x^{2})+(-x-3x)+(1+2)$

$M(x)+N(x)= 2x^{4}+7x^{3}-3x^{2}-4x+3$

+) $M(x)-N(x)=(x^{4}+5x^{3}-x^{2}-x+1)-(x^{4}+2x^{3}-2x^{2}-3x+2)$

$M(x)-N(x)= (x^{4}-x^{4})+(5x^{3}-2x^{3})+(-x^{2}+2x^{2})+(-x+3x)+(1-2)$

$M(x)-N(x)= 3x^{3}+x^{2}+2x-1$

Câu 3: Cho hai đa thức:

$A(x)=5x^{5}+3x-4x^{4}-2x^{3}+6-4x^{2}$ ; $B(x)= 2x^{4}-x+3x^{2}-2x^{3}+\frac{1}{4}-x^{5}$

a) Sắp xếp các đa thức trên theo luỹ thừa giảm dần của biến x.

b) Tính A(x) + B(x) và A(x) – B(x)

Giải:

a) $A(x)=5x^{5}+3x-4x^{4}-2x^{3}+6-4x^{2}$;

$=5x^{5}-4x^{4}-2x^{3}-4x^{2}+3x+6$

$B(x)=2x^{4}-x+3x^{2}-2x^{3}+\frac{1}{4}-x^{5}$

$=-x^{5}+2x^{4}-2x^{3}+3x^{2}-x+\frac{1}{4}$

b) 

+)$A(x)+B(x)=(5x^{5}-4x^{4}-2^{3}-4x^{2}+3x+6)+(-x^{5}+2x^{4}-2x^{3}+3x^{2}-x+\frac{1}{4})$

$A(x)+B(x)=(5x^{5}-x^{5})+(-4x^{4}+2x^{4})+(-2x^{3}-2x^{3})+(-4x^{2}+3x^{2})+(3x-x)+(6+\frac{1}{4})$

$A(x)+B(x)=(5x^{5}-x^{5})+(-4x^{4}+2x^{4})+(-2x^{3}-2x^{3})+(-4x^{2}+3x^{2})+(3x-x)+(6+\frac{1}{4})$

$A(x)+B(x)=4x^{5}-2x^{4}-4x^{3}-x^{2}+2x+\frac{25}{4}$

 +)$A(x)-B(x)=(5x^{5}-4x^{4}-2x^{3}-4x^{2}+3x+6)-(-x^{5}+2x^{4}-2x^{3}+3x^{2}-x+\frac{1}{4})$

$A(x)-B(x)=(5x^{5}+x^{5})+(-4x^{4}-2x^{4})+(-2x^{3}+2x^{3})+(-4x^{2}-3x^{2})+(3x+x)+(6-\frac{1}{4})$

$A(x)-B(x)=6x^{5}-6x^{4}-7x^{2}+4x+\frac{23}{4}$

Câu 4: Cho hai đa thức: 

$A(x)=5x^{5}+2x^{2}-\frac{1}{2}x-3$; $B(x)=-x^{5}-3x^{2}+\frac{1}{2}x+1$

a) Tính M(x) = A(x)+B(x)

b) Tính N(x) = A(x) – B(x)

Giải:

a) $M(x)=A(x)+B(x)$

$=(5x^{5}+2x^{2}-\frac{1}{2}x-3)+(-x^{5}-3x^{2}+\frac{1}{2}x+1)$

$=(5x^{5}-x^{5})+(2x^{2}-3x^{2})+(-\frac{1}{2}x+\frac{1}{2}x)+(-3+1)$

$=4x^{5}-x^{2}-2$

b) $N(x)=A(x)-B(x)$

$=(5x^{5}+2x^{2}-\frac{1}{2}x-3)-(-x^{5}-3x^{2}+\frac{1}{2}x+1)$

$=(5x^{5}+x^{5})+(2x^{2}+3x^{2})+(-\frac{1}{2}x-\frac{1}{2}x)+(-3-1)$

 $6x^{5}+5x^{2}-x-4$

Câu 5. Tính:

a) $3x^{2}-4y^{2}+6xy+7+(-x^{2}+y^{2}-8xy+9x+1)$

b) $4x^{2}y-2xy^{2}+8-(3x^{2}y+9xy^{2}-12xy+6)$

Giải:

a) $3x^{2}-4y^{2}+6xy+7+(-x^{2}+y^{2}-8xy+9x+1)$

$=3x^{2}-4y^{2}+6xy+7-x^{2}+y^{2}-8xy+9x+1$

$=2x^{2}-3y^{2}-2xy+9x+8$

b) $4x^{2}y-2xy^{2}+8-(3x^{2}y+9xy^{2}-12xy+6)$

 $=4x^{2}y-2xy^{2}+8-3x^{2}y-9xy^{2}+12xy-6$

$=x^{2}y-11xy^{2}+12xy+2$

2. THÔNG HIỂU (6 câu)

Câu 1. Cho các đa thức: 

$A=4x^{2}-5xy+3y^{2}$

$B=3x^{2}+2xy+y^{2}$

$C=-x^{2}+3xy+2y^{2}$

Tính A + B + C; B – C – A; C – A – B

Giải:

a) +) $A+B+C=(4x^{2}-5xy+3y^{2})+(3x^{2}+2xy+y^{2})+(-x^{2}+3xy+2y^{2})$

$A+B+C=(4x^{2}+3x^{2})+(-5xy+2xy)+(3y^{2}+2y^{2})$

$A+B+C=7x^{2}-3xy+5y^{2}$

+) $B-C-A=(3x^{2}+2xy+y^{2})-(-x^{2}+3xy+2y^{2})-(4x^{2}-5xy+3y^{2})$

$B-C-A=(3x^{2}+x^{2}-4x^{2})+(2xy-3xy+5xy)+(y^{2}-2y^{2}-3y^{2})$

$B-C-A=4xy-4y^{2}$

+) $C-A-B=(-x^{2}+3xy+2y^{2})-(4x^{2}-5xy+3y^{2})-(3x^{2}+2xy+y^{2})$

 $C-A-B=(-x^{2}-4x^{2}-3x^{2})+(3xy+5xy-2xy)+(2y^{2}-3y^{2}-y^{2})$

$C-A-B=-8x^{2}+6xy-2y^{2}$

Câu 2. Tìm tồng A+B và hiệu A-B của hai đa thức rồi tìm bậc của chúng biết:

$A=2x^{3}-4x^{2}y+1\frac{1}{3}xy^{2}-y^{4}+1;B=-2x^{3}-1\frac{1}{2}x^{2}y-y^{4}-3$

Giải:

$A+B=(2x^{3}-4x^{2}y+1\frac{1}{3}xy^{2}-y^{4}+1)+(-2x^{3}-1\frac{1}{2}x^{2}y-y^{4}-3)=-2y^{4}-\frac{11}{2}x^{2}y+\frac{4}{3}xy^{2}-2$

Do đó tồng hai đa thức có bậc là 4 .

$A-B=(2x^{3}-4x^{2}y+1\frac{1}{3}xy^{2}-y^{4}+1)-(-2x^{3}-1\frac{1}{2}x^{2}y-y^{4}-3)=4x^{3}-\frac{5}{2}x^{2}y+\frac{4}{3}xy^{2}+4$

Do đó hiệu hai đa thức có bậc là 3 .

Câu 3: Cho hai đa thức: $A=x^{2}-4x+1;B=2x^{2}+2x$

a) Tính C=A+B
b) Tìm bậc của C
c) Tính giá trị C của tại x=-1
Giải:

a) Ta có:

$C=(x^{2}-4x+1)+(2x^{2}+2x)$

$=x^{2}-4x+1+2x^{2}+2x$

$=(x^{2}+2x^{2})+(-4x+2x)+1$

$=3x^{2}-2x+1$

b) Bậc của C bằng 2 .

c) Thay x=-1 vào C ta được $C=3.(-1)^{2}-2.(-1)+1=6$.

Câu 4: Tính giá trị của biểu thức:

a) $3x^{2}y-(3xy-6x^{2}y)+(5xy-9x^{2}y)$ tại $x=\frac{2}3{};y=\frac{-3}{4}$

b) $x(x-2y)-y(y^{2}-2x)$ tại x = 5, y = 3

Giải:

a) $3x^{2}y-(3xy-6x^{2}y)+(5xy-9x^{2}y)=3x^{2}y-3xy+6x^{2}y+5xy-9x^{2}y=2xy$

Thay  $x=\frac{2}{3},y=\frac{-3}{4}$ vào biểu thức ta có: 2 ×$\frac{2}{3}$ ×$\frac{-3}{4}$= −1

b) $x(x-2y)-y(y^{2}-2x)=x^{2}-2xy-y^{3}+2xy=x^{2}-y^{3}$

Thay x = 5, y = 3 vào biểu thức ta có: $5^{2}-3^{3}=-2$

Câu 5. Tìm biết:
a) $M+(5x^{2}-2xy)=6x^{2}+9xy-y^{2}$
b) $M-(6x^{2}-4xy)=7x^{2}-8xy+y^{2}$

Giải:

a) Ta có $M=(6x^{2}+9xy-y^{2})-(5x^{2}-2xy)$

$=6x^{2}+9xy-y^{2}-5x^{2}+2xy$

$=(6x^{2}-5x^{2})+(9xy+2xy)-y^{2}$

$=x^{2}+11xy-y^{2}$

b) Ta có: $M=(7x^{2}-8xy+y^{2})+(6x^{2}-4xy)$

 $7x^{2}-8xy+y^{2}+6x^{2}-4xy$

$(7x^{2}+6x^{2})+(-8xy-4xy)+y^{2}$

$=13x^{2}-12xy+y^{2}$

Câu 6: Tìm biết:
a) $3ab^{2}-b^{2}a-A=ab+b^{2}a$
b) $2A+x^{2}+3x+1=3x^{2}-x+3$
Giải:

a)$3ab-b^{2}a-A=ab+b^{2}a$

$A=3ab-b^{2}a-ab-b^{2}a$

$=2ab-2b^{2}a$

b) $2A+x^{2}+3x+1=3x^{2}-x+3$

$2A=(3x^{2}-x+3)-(x^{2}+3x+1)$

$2A=2x^{2}-4x+2$

 $A=x^{2}-2x+1$

3. VẬN DỤNG (6 câu)

Câu 1: Tìm độ dài cạnh còn thiếu của tam giác ở Hình 7, biết rằng tam giác có chu vi bằng 7x + 5y

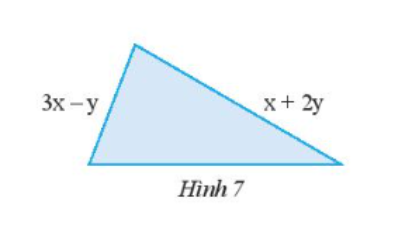
Giải:

Độ dài cạnh còn lại là: 7x + 5y - (3x - y + x + 2y) = 7x + 5y - 3x + y - x - 2y = 3x + 4y

Câu 2: a) Rút gọn rồi tính giá trị của biểu thức.

$P=(5x^{2}-2xy+y^{2})-(x^{2}+y^{2})-(4x^{2}-5xy+1)$ khi x=1,2 và x+y=6,2

b) Chứng minh giá trị của biểu thức sau không phụ thuộc vào giá trị của biến x.

$(x^{2}-5x+4)(2x+3)-(2x^{2}-x-10)(x-3)$

Giải:

a) Rút gọn rồi tính giá trị của biểu thức.

$P=(5x^{2}-2xy+y^{2})-(x^{2}+y^{2})-(4x^{2}-5xy+1)$

$=5x^{2}-2xy+y^{2}-x^{2}-y^{2}-4x^{2}+5xy-1$

$=(5x^{2}-x^{2}-4x^{2})-(2xy-5xy)+(y^{2}-y^{2})-1$

$=0+3xy-1=3xy$

Khi x=1,2 và x+y=6,2 => y = 6,2 - 1,2=5.

Vậy giá trị của P = 3.1,2.5=18

b) Ta có:

$(x^{2}-5x+4)(2x+3)-(2x^{2}-x-10)(x-3)$

$=x^{2}.2x+x^{2}.3-5.2.x.x-5x.3+4.2x+4.3-(2x^{2}.x-2.(-3).x^{2}-x.x+3x-10x+10.3)$

$=2x^{2}+1+3x^{2}-10x^{2}-15x+8x+12-2x^{2}+1+6.x^{2}+x^{2}-3x+10x-30$

$=(2x^{3}-2x^{3})+(3x^{2}+6.x^{2}+x^{2}-10x^{2})-(15x-8x+3x-10x)-30+12=-18$

Như vậy giá trị của biểu thức luôn là 18 và không phụ thuộc vào giá trị của biến x

Câu 3: 

a) Chứng minh rằng biểu thức $P=5x(2-x)-(x+1)(x+9)$ luôn nhận giá trị âm với mọi giá trị của biến x.

b) Chứng minh rằng biểu thức $Q=3x^{2}+x(x-4y)-2x(6-2y)+12x+1$ luôn nhận giá trị dương với mọi giá trị của biến x và y.

Giải:

a. Ta có: 

$P=5x(2-x)-(x+1)(x+9)=5.2.x-5.x.x-(x.x+x.9+1.x+1.9)$

$=10x-5x^{2}-x^{2}-9x-x-9=-6x^{2}-9$

Vì $x^{2}\geq 0\Rightarrow -6x^{2}\leq 0\Rightarrow -6x^{2}-9\leq 0$

Vậy P luôn nhận giá trị âm với mọi giá trị của biến x.

b.Ta có: 

$Q=3x^{2}+x(x-4y)-2x(6-2y)+12x+1$

$=3x^{2}+x.x-4.x.y-2.6x+2.2.x.y+12x+1$

$=3x^{2}+x^{2}-4xy-12x+4xy+12x+1=4x^{2}+1$

Vì $x^{2}\geq 0\Rightarrow 4x^{2}\geq 0\Rightarrow 4x^{2}+1\geq 1$

Vậy Q luôn nhận giá trị dương với mọi giá trị của biến x và y.

Câu 4. Cho: $A=x^{2}yz;B=xy^{2}z;C=x^{z}$ và $x+y+z=1$ Hãy chứng tỏ: A+B+C=xyz

Giải:

Ta có : $A+B+C=x^{2}yz+y^{2}z+xyz^{2}=xyz(x+y+z)$
Mà $x+y+z=1$ nên $A+B+C=xyz.1=xyz$

Bài 5. Cho hai đa thức $P(x)=2x^{3}-2x+x^{2}-x^{3}+3x+2$ và $Q(x)=4x^{3}-5x^{2}+3x-4x-3x^{3}+4x^{2}+1$
a. Rút gọn và sắp xếp các đa thức theo lũy thừa giảm dần của biến .
b. Tính $P(x)+Q(x);P(x)-Q(x)$
c. Tính $P(-1);Q(2)$

Giải:

a) Rút gọn và sắp xếp

$P(x)=x^{3}+x^{2}+x+2$

$Q(x)=x^{3}-x^{2}-x+1$

b) $P(x)+Q(x)=2x^{3}+3$

$P(x)-Q(x)=2x^{2}=2x+1$

c) $P(-1)=(-1)^{3}+(-1)^{2}+(-1)+2=1$

$Q(2)=2^{3}-2^{2}-2+1=3$

Bài 6. Cho các đa thức

$M(x)=3x^{3}-2x+4x^{2}-x+5;N(x)=2x^{2}-x+3x^{3}-3c^{2}+9$

Biết $M(x)+N(x)-P(x)=6x^{3}+3x^{2}+2x$. Hãy tìm đa thức P(x)

Giải:

$P(x)=M(x)+N(x)-(6x^{3}+3x^{2}+2x)$

……..

Ta tìm được $P(x)=-6x+14$

4. VẬN DỤNG CAO (2 câu)

Câu 1: Cho đa thức $P(x)=ax^{2}+bx+c(a\in N^{*})$ thỏa mãn $P(9)-P(6)=2019$. Chứng minh $P(10)-P(7)$ là một số lẻ.
Giải:

Ta có:

$P(9)-P(6)=2019$

$\Leftrightarrow (8ba+9b+c)-(36a+6b+c)=2019$

$\Leftrightarrow 45a+3b=2019(1)$

Lại có: $P(10)-P(7)=(100a+10b+c)-(29a+7b+c)=51a+3b$

Đặt $P(10)-P(7)=t\Rightarrow 51a+3b=t(2)$

Trừ vế theo vế (2) cho (1) ta có: 6a=t-2019, mà 6a chẵn, 2019 lẻ nên t lẻ, ta có điều phải chứng minh

Câu 2. Cho đa thức P(x) thỏa mãn:

$P(1)=1;P(\frac{1}{x})=\frac{1}{x^{2}}P(x),\forall x\neq 0;P(x_{1}+x_{2})=P(x_{1})+P(x_{2}),\forall x_{1},x_{2}\in R$

Tính P $\left ( \frac{2}{7} \right )$

Giải:

Ta có: $P(2)=P(1+1)=P(1)+P(1)=1+1+2$
Tương tư: $P(3)=3;P(5)=5;P(7)=7$
Tù đó: $P\left ( \frac{1}{7} \right )=\frac{1}{7^{2}}P(7)=\frac{1}{7};P\left ( \frac{2}{7} \right )=P\left ( \frac{1}{7} \right )+P\left ( \frac{1}{7} \right )=\frac{2}{7}$
Tương tự: $P\left ( \frac{3}{7} \right )=\frac{3}{7};P\left ( \frac{5}{7} \right )=\frac{5}{7}$